题目内容
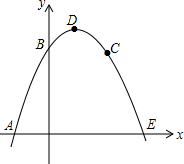 抛物线经过A(-1,0)、B(0,3)、C(2,3)三点,顶点为D,且与x轴的另一个交点为E.
抛物线经过A(-1,0)、B(0,3)、C(2,3)三点,顶点为D,且与x轴的另一个交点为E.(1)求该抛物线的解析式;
(2)求E点的坐标.
考点:待定系数法求二次函数解析式,抛物线与x轴的交点
专题:计算题
分析:(1)设一般式y=ax2+bx+c,再把A、B、C三点的坐标代入得到关于a、b、c的方程组,然后解方程组求出a、b、c的值,从而得到抛物线解析式;
(2)根据抛物线与x轴的交点问题,通过解方程-x2+2x+3=0即可得到点E的坐标.
(2)根据抛物线与x轴的交点问题,通过解方程-x2+2x+3=0即可得到点E的坐标.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,
把A(-1,0)、B(0,3)、C(2,3)分别代入得
,解得
,
所以抛物线的解析式为y=-x2+2x+3;
(2)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,
所以E点坐标为(3,0).
把A(-1,0)、B(0,3)、C(2,3)分别代入得
|
|
所以抛物线的解析式为y=-x2+2x+3;
(2)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,
所以E点坐标为(3,0).
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
四个数-3,-2,1,0.5中,相反数最小的是( )
| A、-3 | B、-2 | C、1 | D、0.5 |
 一只自由飞行的小鸟,将随意地落在如图所示方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为
一只自由飞行的小鸟,将随意地落在如图所示方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为 如图,一轮船在海上以每小时30海里的速度向西方向航行,上午8时,在B处测得小岛A在北偏东30°方向,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A在北偏东60°方向.如果轮船仍继续向正西方向航行,于上午11时到达D处,这时轮船与小岛A相距多远?
如图,一轮船在海上以每小时30海里的速度向西方向航行,上午8时,在B处测得小岛A在北偏东30°方向,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A在北偏东60°方向.如果轮船仍继续向正西方向航行,于上午11时到达D处,这时轮船与小岛A相距多远?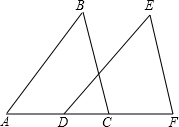 已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.