题目内容
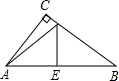如图，△ABC中，∠C=90°，DE是AB的垂直平分线，且∠CAD：∠CAB=1：5，则∠B=________°．
40
分析：设∠CDA=x，根据∠CAD：∠CAB=1：5，得到∠DAB=4x，再根据线段的垂直平分线的性质得到DA=DB，则∠DAB=∠B=4x，然后利用三角形的内角和定理求出x，即可得到∠B的度数．
解答：设∠CDA=x，
∵∠CAD：∠CAB=1：5，
∴∠DAB=4x，
又∵DE是AB的垂直平分线，
∴DA=DB，
∴∠DAB=∠B=4x，
∴5x+4x=90°，
解得x=10°，
∴∠B=40°．
故答案为：40．
点评：本题考查了线段的垂直平分线的性质：线段垂直平分线上的点到线段两端点的距离相等．也考查了三角形的内角和定理．
分析：设∠CDA=x，根据∠CAD：∠CAB=1：5，得到∠DAB=4x，再根据线段的垂直平分线的性质得到DA=DB，则∠DAB=∠B=4x，然后利用三角形的内角和定理求出x，即可得到∠B的度数．
解答：设∠CDA=x，
∵∠CAD：∠CAB=1：5，
∴∠DAB=4x，
又∵DE是AB的垂直平分线，
∴DA=DB，
∴∠DAB=∠B=4x，
∴5x+4x=90°，
解得x=10°，
∴∠B=40°．
故答案为：40．
点评：本题考查了线段的垂直平分线的性质：线段垂直平分线上的点到线段两端点的距离相等．也考查了三角形的内角和定理．
练习册系列答案
中考解读考点精练系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．