Question

点P（x，y）在第一象限，且x+y=10，点A的坐标为（8，0），设原点为O，△OPA的面积为S．

（1）求S与x的函数关系式，写出x的取值范围，画出这个函数图象；

（2）当S=12时，求点P的坐标；

（3）△OPA的面积能大于40吗？为什么？

Answer 1

解：（1）∵A和P点的坐标分别是（8，0）、（x，y），

∴△OPA的面积=OA•|y_P|，∴S=×8×|y|=4y．

∵x+y=10，∴y=10﹣x．∴S=4（10﹣x）=40﹣4x；

∵S=﹣4x+40＞0，解得：x＜10；

又∵点P在第一象限，∴x＞0，即x的范围为：0＜x＜10；

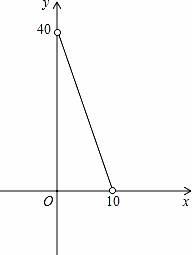
∵S=﹣4x+40，S是x的一次函数，

∴函数图象经过点（10，0），（0，40）．

所画图象如下：

（2）∵S=﹣4x+40，∴当S=12时，12=﹣4x+40， 解得：x=7，y=3． 即当点P的坐标为（7，3）； （3）△OPA的面积不能大于40．理由如下： ∵S=﹣4x+40，﹣4＜0， ∴S随x的增大而减小， 又∵x=0时，S=40， ∴当0＜x＜10，S＜40． 即△OPA的面积不能大于40．