题目内容
【题目】定义:若两条抛物线在x轴上经过两个相同点,那么我们称这两条抛物线是“同交点抛物线”,在x轴上经过的两个相同点称为“同交点”,已知抛物线y=x2+bx+c经过(﹣2,0)、(﹣4,0),且一条与它是“同交点抛物线”的抛物线y=ax2+ex+f经过点(﹣3,3).
(1)求b、c及a的值;
(2)已知抛物线y=﹣x2+2x+3与抛物线yn=![]() x2﹣
x2﹣![]() x﹣n(n为正整数)
x﹣n(n为正整数)
①抛物线y和抛物线yn是不是“同交点抛物线”?若是,请求出它们的“同交点”,并写出它们一条相同的图像性质;若不是,请说明理由.
②当直线y=![]() x+m与抛物线y、yn,相交共有4个交点时,求m的取值范围.
x+m与抛物线y、yn,相交共有4个交点时,求m的取值范围.
③若直线y=k(k<0)与抛物线y=﹣x2+2x+3与抛物线yn =![]() x2﹣
x2﹣![]() x﹣n (n为正整数)共有4个交点,从左至右依次标记为点A、点B、点C、点D,当AB=BC=CD时,求出k、n之间的关系式
x﹣n (n为正整数)共有4个交点,从左至右依次标记为点A、点B、点C、点D,当AB=BC=CD时,求出k、n之间的关系式
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①是“同交点抛物线”,“同交点”为:(–1,0)、(3,0),它们图形共同性质有:对称轴同为直线
;(2)①是“同交点抛物线”,“同交点”为:(–1,0)、(3,0),它们图形共同性质有:对称轴同为直线![]() ;②
;②![]() ,且
,且![]() ,
,![]() ;③
;③![]()
【解析】
(1)将(–2,0)、( –4,0)代入![]() ,即可求得b、c的值,设“同交点抛物线”的解析式为
,即可求得b、c的值,设“同交点抛物线”的解析式为![]() ,将(–3,3)代入即可求得
,将(–3,3)代入即可求得![]() 的值;
的值;
(2)①令![]() 和
和![]() ,分别求得与
,分别求得与![]() 轴的交点坐标,即可作出判断;
轴的交点坐标,即可作出判断;
②先求得直线![]() 与抛物线
与抛物线![]() 或抛物线
或抛物线![]() 只有一个交点时
只有一个交点时![]() 的值,除去直线
的值,除去直线![]() 经过“同交点”时的
经过“同交点”时的![]() 的值,即可求解;
的值,即可求解;
③由![]() 和
和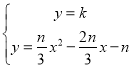 利用根与系数的关系求得
利用根与系数的关系求得![]() 和
和![]() 的值,再根据
的值,再根据![]() ,得到
,得到![]() 即可求得答案.
即可求得答案.
(1) ∵抛物线![]() 经过(–2,0)、( –4,0),则代入得:
经过(–2,0)、( –4,0),则代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
设“同交点抛物线”的解析式为![]() ,
,
将(–3,3)代入得:![]() ,
,
解得:![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)①令![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴抛物线![]() 与
与![]() 轴的交点坐标为:(–1,0)、(3,0),
轴的交点坐标为:(–1,0)、(3,0),
令![]() ,则
,则![]()
![]()
![]()
![]() ,
,
解得:![]() ,
,
∴抛物线![]() 与
与![]() 轴的交点坐标为:(–1,0)、(3,0),
轴的交点坐标为:(–1,0)、(3,0),
∴抛物线![]() 和抛物线
和抛物线![]() 是“同交点抛物线”,
是“同交点抛物线”,
它们图形共同性质:对称轴同为直线![]() ;
;
②当直线![]() 与抛物线y相交只有1个交点时,
与抛物线y相交只有1个交点时,
由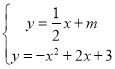 ,得:
,得:![]() ,
,
由![]() ,
,
解得:![]() ,
,
抛物线![]() 的顶点坐标为(1,
的顶点坐标为(1,![]() ),其中
),其中![]() 为正整数,
为正整数,
因为随着![]() 的增大,
的增大,![]() 的顶点纵坐标减小,所以当直线
的顶点纵坐标减小,所以当直线![]() 与抛物线
与抛物线![]() 中
中![]() 时的抛物线相交只有1个交点时,
时的抛物线相交只有1个交点时,
由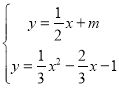 ,得:
,得:![]() ,
,
由![]() ,
,
解得:![]() ,
,
如图所示:
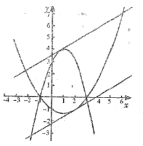
当直线![]() 经过“同交点”时与两抛物线只有三个交点,
经过“同交点”时与两抛物线只有三个交点,
把“同交点”(–1,0)代入![]() 得:
得:![]() ,
,
把“同交点” (3,0)代入![]() 得:
得:![]() ,
,
∴当直线![]() 与抛物线
与抛物线![]() 、
、![]() 有4个交点时,m的取值范围为:
有4个交点时,m的取值范围为:
![]() ,且
,且![]() ,
,![]() ;
;
③设直线![]() 分别与抛物线
分别与抛物线![]() 和抛物线
和抛物线![]() 相交于A、D、B、C,如图:
相交于A、D、B、C,如图:
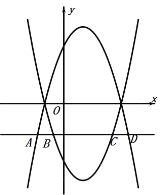
由![]() ,得:
,得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
由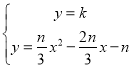 ,得:
,得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案