题目内容
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
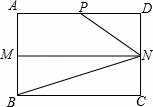
(1)由MN∥BC,易得∠CBN=∠MNB,由已知∠PNB=3∠CBN,根据角的和差不难得出结论;
(2)连接AN,根据矩形的轴对称性,可知∠PAN=∠CBN,由(1)知∠PNM=2∠CBN=2∠PAN,由AD∥MN,可知∠PAN=∠ANM,所以∠PAN=∠PNA,根据等角对等边得到AP=PN,再用勾股定理列方程求出AP.
解答: 解:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN∥BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN;
(2)连接AN,
根据矩形的轴对称性,可知∠PAN=∠CBN,
∵MN∥AD,
∴∠PAN=∠ANM,
由(1)知∠PNM=2∠CBN,
∴∠PAN=∠PNA,
∴AP=PN,
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2,
设AP=x,则PD=6﹣x,
在Rt△PDN中
PD2+DN2=PN2,
∴(6﹣x)2+22=x2,
解得:x=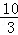
所以AP=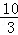 .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
下列各数表示正确的是( )
|
| A. | 57000000=57×106 |
|
| B. | 0.0158(用四舍五入法精确到0.001)=0.015 |
|
| C. | 1.804(用四舍五入法精确到十分位)=1.8 |
|
| D. | 0.0000257=2.57×10﹣4 |
 )﹣2+(2﹣
)﹣2+(2﹣ )0﹣|﹣2|.
)0﹣|﹣2|. 的自变量x的取值范围是
的自变量x的取值范围是  >bc
>bc ﹣2a>﹣2b
﹣2a>﹣2b