Question

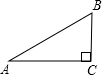如图，Rt△ABC中，∠C=90°，∠A=30°，AB=2．
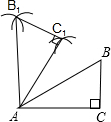
（1）用尺规作图，作出△ABC绕点A逆时针旋转60°后得到的△AB₁C₁（不写画法，保留画图痕迹）；结论：______为所求．
（2）在（1）的条件下，连接B₁C，求B₁C的长．

Answer 1

解：（1）所画图形如下所示：

（2）

∵∠A=30°，AB=2，
∴BC=1，
∴AC=4-1=3，
由（1）得：∠B₁AC=60°，
又AB=AB₁=2，
∴B₁C²=AB₁²+AC²=7，
∴B₁C=．
分析：（1）分别以C点为圆心，以AC为半径，以B点为圆心，以AB为半径画圆，交点分别为C、B，连接即可；
（2）先求出BC的长，然后根据AB=AB₁=2，再利用勾股定理即可得出答案．
点评：本题考查运用尺规作图法旋转图形及勾股定理的应用，有一定难度，关键是掌握旋转后的图形与原图形全等．