题目内容
(1999•黄冈)分解因式(ax+by)2+(bx-ay)2= .
【答案】分析:先根据完全平方公式展开,合并同类项后再两两分组,然后两次提取公因式分解即可.
解答:解:(ax+by)2+(bx-ay)2,
=a2x2+b2y2+2abxy+b2x2+a2y2-2abxy,
=a2x2+b2x2+b2y2+a2y2,
=(a2+b2)x2+(a2+b2)y2,
=(a2+b2)(x2+y2).
故答案为:(a2+b2)(x2+y2).
点评:本题考查了分组分解法分解因式,先根据完全平方公式计算,合并同类项后再分组分解因式.
解答:解:(ax+by)2+(bx-ay)2,
=a2x2+b2y2+2abxy+b2x2+a2y2-2abxy,
=a2x2+b2x2+b2y2+a2y2,
=(a2+b2)x2+(a2+b2)y2,
=(a2+b2)(x2+y2).
故答案为:(a2+b2)(x2+y2).
点评:本题考查了分组分解法分解因式,先根据完全平方公式计算,合并同类项后再分组分解因式.

练习册系列答案
相关题目
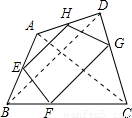
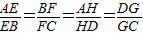 =k(k>0).阅读下段材料,回答下列问题:
=k(k>0).阅读下段材料,回答下列问题: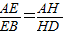 ,∴EH∥BD,∵
,∴EH∥BD,∵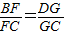 ,∴FG∥BD,∴FG∥EH.
,∴FG∥BD,∴FG∥EH.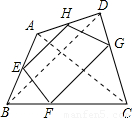
 =k(k>0).阅读下段材料,回答下列问题:
=k(k>0).阅读下段材料,回答下列问题: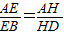 ,∴EH∥BD,∵
,∴EH∥BD,∵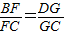 ,∴FG∥BD,∴FG∥EH.
,∴FG∥BD,∴FG∥EH.