题目内容
如图，点A、C在反比例函数
的图象上，B、D在x轴上，△OAB，△BCD均为正三角形，则点C的坐标是________．
（1+
，
）
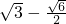分析：如图，过A作AM⊥OB于M，设点A（a，b），则根据已知条件得到a•b=
，OB=-2a，OM=a，AM=-b，又△OAB为正三角形，由此可以得到AM=
OM，然后即可求出OB=2，设点C（m，n），再用n同样的方法可以求m的值，然后即可求出C的坐标．
解答：
解：如图，过A作AM⊥OB于M，
设点A（a，b），
则a•b=①，
OB=2a，OM=a，AM=b，
又△OAB为正三角形，
∴AM=OM，
∴b=a②，
联立①②即可求出a=
∴OB=
，
设点C（m，n），
则n=（m-），
∴m•（m-）=，
∴m=1+，n=．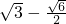
故答案为：（1+，）．
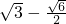点评：此题难度中等，既考查反比例函数的性质，又考查等边三角形性质，还考查利用坐标表示线段长．
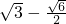，）分析：如图，过A作AM⊥OB于M，设点A（a，b），则根据已知条件得到a•b=
，OB=-2a，OM=a，AM=-b，又△OAB为正三角形，由此可以得到AM=OM，然后即可求出OB=2，设点C（m，n），再用n同样的方法可以求m的值，然后即可求出C的坐标．解答：
解：如图，过A作AM⊥OB于M，设点A（a，b），
则a•b=
①，OB=2a，OM=a，AM=b，
又△OAB为正三角形，
∴AM=
OM，∴b=
a②，联立①②即可求出a=
∴OB=
，设点C（m，n），
则n=
（m-），∴m•
（m-）=，∴m=1+
，n=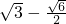．故答案为：（1+
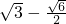，）．点评：此题难度中等，既考查反比例函数的性质，又考查等边三角形性质，还考查利用坐标表示线段长．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
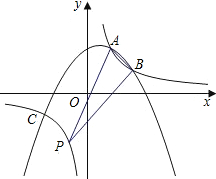如图，抛物线y=ax2+bx+c经过点A（1，2）、B（2，1）和C（-2，-1）三点．
如图，△P1OA1，△P2A1A2，△P3A2A3，…，是等腰直角三角形，点P1，P2，P3，…，在反比列函数y=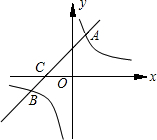
次函数y=mx+b的图象与x轴交于点C．
如图，△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形，点P1、P2、P3、…、P100在反比列函数