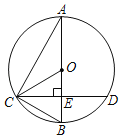
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高.
边上的高.
问题发现:
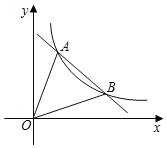
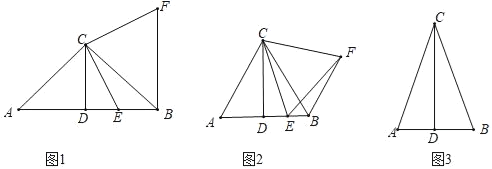
(1)如图1,若![]() ,点
,点![]() 是线段
是线段![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合)连接
重合)连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,我们会发现
,我们会发现![]() 、
、![]() 、
、![]() 之间的数量关系是
之间的数量关系是![]() ,请你证明这个结论;
,请你证明这个结论;
提出猜想:
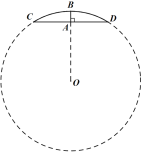
(2)如图2,若![]() ,点
,点![]() 是线段
是线段![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合)连接
重合)连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,猜想线段
,猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系是_______;
之间的数量关系是_______;
拓广探索:
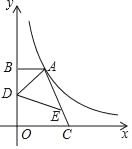
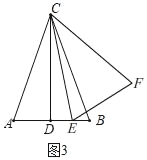
(3)若![]() ,
,![]() (
(![]() 为常数),点
为常数),点![]() 是线段
是线段![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() .请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.
.请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.
【答案】(1)详见解析;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)依据等角的余角相等得到∠ACE=∠BCF,进而由旋转的性质可得CE=CF,至此结合SAS易证得△ACE≌△BCF,则有AE=BF,利用BE+AE=AB可得到BE+BF=AB;
(2)由于△ABC是等腰直角三角形,根据直角三角形斜边上中线的性质得到CD=12AB,由此再进行等量代换即可得到CD、BF、BE之间的数量关系;
(3)结合题意可知△ABC为等边三角形,则有CD=3![]() AB,至此再结合BE+BF=AB即可解答本题,同理可求解.
AB,至此再结合BE+BF=AB即可解答本题,同理可求解.
解:(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由旋转知,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]()
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]()
由旋转知,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(3)如图3,
由旋转知,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.

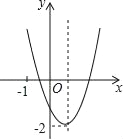
【题目】二次函数![]() (
(![]() ,
,![]() 是常数)中,自变量
是常数)中,自变量![]() 与函数
与函数![]() 的对应值如下表:
的对应值如下表:
| -1 |
| 0 |
| 1 |
| 2 |
| 3 |
|
|
| 1 |
| 2 |
| 1 |
| -2 |
(1)判断二次函数图象的开口方向,并写出它的顶点坐标;
(2)一元二次方程![]() (
(![]() ,
,![]() 是常数)的两个根
是常数)的两个根![]() ,
,![]() 的取值范围是下列选项中的哪一个 .
的取值范围是下列选项中的哪一个 .
A.![]() B.
B.![]()
C. ![]() D.
D.![]()