题目内容
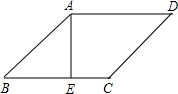
菱形ABCD中，AE⊥BC于E，AF⊥CD于F，求证：AE=AF．
证明：∵AE⊥BC于E，AF⊥CD于F，
∴∠AEB=∠AFD=90°，
∵菱形ABCD，
∴AB=AD，∠B=∠D．
在Rt△EBA和Rt△FDA中，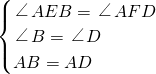
∴△EBA≌△FDA．
∴AE=AF．
分析：根据菱形的性质可以证得：AB=AD，∠B=∠D，即可证得△EBA≌△FDA，根据全等三角形的对应边相等即可证得．
点评：本题主要考查了菱形的性质以及全等三角形的判定与应用，证明线段相等常用的方法是转化为证明三角形全等．
∴∠AEB=∠AFD=90°，
∵菱形ABCD，
∴AB=AD，∠B=∠D．
在Rt△EBA和Rt△FDA中，
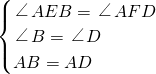
∴△EBA≌△FDA．
∴AE=AF．
分析：根据菱形的性质可以证得：AB=AD，∠B=∠D，即可证得△EBA≌△FDA，根据全等三角形的对应边相等即可证得．
点评：本题主要考查了菱形的性质以及全等三角形的判定与应用，证明线段相等常用的方法是转化为证明三角形全等．
练习册系列答案
相关题目
在菱形ABCD中，AE⊥BC，AF⊥CD，且E，F分别为BC，CD的中点，那么∠EAF的度数为（ ）
| A、75° | B、60° | C、45° | D、30° |
如图，在菱形ABCD中，AE⊥BC于E，已知EC=1，cosB=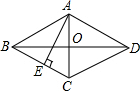
菱形ABCD中，AE垂直平分BC，垂足为E，AB=4cm．那么，菱形ABCD的面积是