题目内容
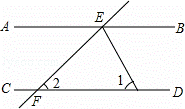
已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，
（1）证明四边形ABDF是平行四边形；
（2）若AF=DF=5，AD=6，求AC的长．
（1）证明：∵BD垂直平分AC，
∴AB=BC，AD=DC，
在△ADB与△CDB中，
，
∴△ADB≌△CDB（SSS）
∴∠BCD=∠BAD，
∵∠BCD=∠ADF，
∴∠BAD=∠ADF，
∴AB∥FD，
∵BD⊥AC，AF⊥AC，
∴AF∥BD，
∴四边形ABDF是平行四边形，
（2）解：∵四边形ABDF是平行四边形，AF=DF=5，
∴▱ABDF是菱形，
∴AB=BD=5，
∵AD=6，
设BE=x，则DE=5﹣x，
∴AB2﹣BE2=AD2﹣DE2，
即52﹣x2=62﹣（5﹣x）2
解得：x=
，
∴
=
，
∴AC=2AE=
．
练习册系列答案
相关题目
上，分别经过A、B两点向轴作垂线段，已知S阴影=1，则S1+S2= ．
的解为正数，则m的取值范围是 
