题目内容
11.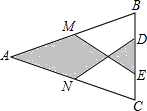 如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=4cm,则图中阴影部分的面积为$\frac{86}{3}$cm2.
如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=4cm,则图中阴影部分的面积为$\frac{86}{3}$cm2.
分析 连接MN,过点A作AG⊥BC于点G,根据等腰三角形的性质求出BG的长,根据勾股定理求出AG的长,再根据三角形中位线定理得出MN的长,由相似三角形的性质求出△AMN的面积,再由相似三角形的性质求出HF及GF的长,根据三角形的面积公式即可得出结论.
解答 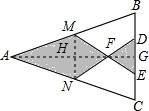 解:连接MN,过点A作AG⊥BC于点G,
解:连接MN,过点A作AG⊥BC于点G,
∵AB=AC,AB=13cm,BC=10cm,
∴BG=$\frac{1}{2}$BC=5cm,
∴AG=$\sqrt{{AB}^{2}-{BG}^{2}}$=$\sqrt{{13}^{2}-{5}^{2}}$=12cm.
∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∴MN=$\frac{1}{2}$BC=5cm,AH=HG=$\frac{1}{2}$AG=6cm,
∴S△AMN=$\frac{1}{2}$×5×6=15cm2.
设GF=x,则HF=6-x,
∵MN∥BC,
∴∠NMF=∠DEF,∠MNF=∠EDF,
∴△MNF∽△EDF,
∴$\frac{DE}{MN}$=$\frac{GF}{HF}$=$\frac{4}{5}$=$\frac{x}{6-x}$,解得x=$\frac{8}{3}$,即GF=$\frac{8}{3}$,HF=6-$\frac{8}{3}$=$\frac{10}{3}$,
∴S△MNF=$\frac{1}{2}$MN•HF=$\frac{1}{2}$×5×$\frac{10}{3}$=$\frac{25}{3}$cm2,S△DEF=$\frac{1}{2}$DE•GF=$\frac{1}{2}$×4×$\frac{8}{3}$=$\frac{16}{3}$cm2,
∴S阴影=S△AMN+S△MNF+S△DEF=15+$\frac{25}{3}$+$\frac{16}{3}$=$\frac{86}{3}$cm2.
故答案为:$\frac{86}{3}$.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | y=$\sqrt{x-1}(x≥1)$ | B. | y=-$\sqrt{x-1}(x≥1)$ | C. | y=$\sqrt{1-x}(x≤1)$ | D. | y=±$\sqrt{1-x}(x≤1)$ |
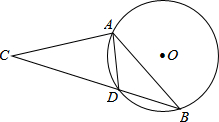 如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | 2 | D. | $\sqrt{3}$+1 |
 如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).
如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).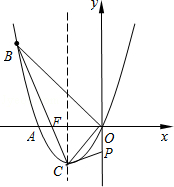 如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.