Question

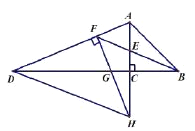
【题目】如图，在等腰直角中， ，的角平分线与的外角平分线交于点，分别交和的延长线于点，过点作交的延长线于点，交的延长线于点，则下列结论:①；②；③为等腰直角三角形:④．其中正确的结论有__________．

Answer 1

【答案】①②③

【解析】

利用等腰直角三角形的内外角平分线的性质得到∠AFB=45°，再利用FH⊥AD易证△FAB≌△FGB，△DFG≌△HFA，从而进行判定．

∵BE是∠ABC的角平分线，AD是∠BAC外角平分线，

∴∠AFB=∠ACB=45°，故①正确；

∵FH⊥AD，

∴∠AFB=∠BFG=45°，

又∵FB=FB，∠ABF=∠FBG，

∴△FAB≌△FGB，

∴FG=FA，

利用角的计算可知，∠FAE=∠FEA=67.5°，

∴FA=FE，

∴FE=FG，故②正确；

∵∠DFG=∠HFA=90°，

FG=FA，易证∠FGD=∠FAH，

∴△DFG≌△HFA，

∴DF=FH，

∴△DFH为等腰直角三角形，故③正确；

由△DFG≌△HFA可得DG=AH，

由△FAB≌△FGB可得BG=AB，

∵BD=DG+GB，BD=AH+AB，故④错误，

故答案为：①②③．