题目内容
 如图,D为△ABC的AB边上的一点,∠DCA=∠B,若AC=
如图,D为△ABC的AB边上的一点,∠DCA=∠B,若AC= cm,AB=3cm,则AD的长为
cm,AB=3cm,则AD的长为
- A.
 cm
cm - B.
 cm
cm - C.2cm
- D.
 cm
cm
C
分析:先判断△ADC与△ACB相似,再利用相似三角形对应边成比例求解即可.
解答:∵∠A=∠A,∠DCA=∠B,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∵AC= cm,AB=3cm,
cm,AB=3cm,
∴AD: =
= :3,
:3,
解得AD=2cm.
故选C.
点评:此题主要考查相似三角形的判定及性质.
分析:先判断△ADC与△ACB相似,再利用相似三角形对应边成比例求解即可.
解答:∵∠A=∠A,∠DCA=∠B,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∵AC=
 cm,AB=3cm,
cm,AB=3cm,∴AD:
 =
= :3,
:3,解得AD=2cm.
故选C.
点评:此题主要考查相似三角形的判定及性质.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
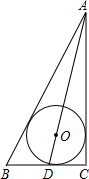 如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )
如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
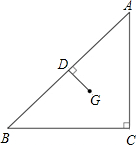 如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )
如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )| A、7 | ||
B、14
| ||
C、
| ||
D、
|
 6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( )
6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( ) 25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?
25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?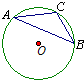 5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=
5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=