��Ŀ����
����Ŀ����֪�����ڽDz�ȷ������ABC�У�AB��AC����E��F�ֱ���AB��AC�ϣ�EF��BC��ƽ���ƶ�EF���������EBCF������Բ��
��![]() ��
��![]() ʱ��sinB��
ʱ��sinB��![]() ��
��
��![]() ��
��![]() ʱ��sinB��
ʱ��sinB��![]() (��ʾ��
(��ʾ��![]() ��
��![]() )����
)����![]() ��
��![]() ʱ��sinB��
ʱ��sinB��![]() ��
��
��1�����������������ӳ�Ĺ��ɣ���գ���![]() ��
��![]() ʱ��sinB��ֵ����______��
ʱ��sinB��ֵ����______��
��2����![]() ��
��![]() ʱ(n�Ǵ���1����Ȼ��)�����ú�n�Ĵ���ʽ��ʾsinB��______��������ͼ�Ρ�д����֪����֤��֤�����̣�
ʱ(n�Ǵ���1����Ȼ��)�����ú�n�Ĵ���ʽ��ʾsinB��______��������ͼ�Ρ�д����֪����֤��֤�����̣�
���𰸡���1��![]() ����2��
����2��![]() ��֤����������
��֤����������
��������
(1) ![]() �ķ�ĸ��1����sinB�ķ�ĸ��sinB�ķ�����2����
�ķ�ĸ��1����sinB�ķ�ĸ��sinB�ķ�����2����![]() �ķ�ĸ������ƽ���������ݹ���ֱ��д���𰸼��ɣ�
�ķ�ĸ������ƽ���������ݹ���ֱ��д���𰸼��ɣ�
(2) ����֪������д����֪����֤���ٽ���֤����
Ҫ���ʾ��sinB����֤����AEM�ס�ABN���ó�![]() ������EM=k����BN=nk����EH��MN��BC��H����HN=EM=k���ɹ��ɶ�����
������EM=k����BN=nk����EH��MN��BC��H����HN=EM=k���ɹ��ɶ�����![]() �����ɵó�sinB��ֵ��
�����ɵó�sinB��ֵ��
�⣺(1)���ݹ��ɣ���![]() ��
��![]() ʱ��
ʱ��
sinB=![]() ��
��
�ʵ�![]() ��
��![]() ʱ��sinB��ֵ����
ʱ��sinB��ֵ����![]() ��
��
(2)![]() ��
��
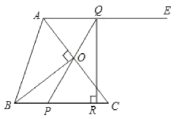
��֪���ڡ�ABC�У�AB��AC��EF��BC����O����������EBCF����D��N��G��MΪ�е㣬![]() ��
��![]() ʱ(n�Ǵ���1����Ȼ��)������ͼ��
ʱ(n�Ǵ���1����Ȼ��)������ͼ��
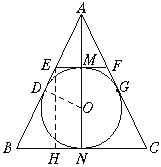
��֤��sinB��![]() ��
��
֤��������AO���ӳ���BC�ཻ��
�ߡ���O����������EBCF��AB��AC�ǡ�O�����ߣ�
�ࡡ��BAO����CAO��
�ߡ�EF��BC��AB��AC��
�ࡡAE��AF��
�֡�M��NΪ�е㣬
�ࡡOM��EF��ON��BC��
�ࡡAO��EF��M��AO��BC��N��
�ߡ�EF��BC��
�ࡡEM��BN��
�ࡡ��AEM�ס�ABN��
�ࡡ![]() ��
��
��EM��k����BN��nk��
��EH��MN��BC��H����HN��EM��k��
�ߡ�D��N��MΪ�е㣬
�ࡡBD��BN��nk��ED��EM��k��
�ڡ�EHB�У���EHB����MNB��90�㣬
BE��BD��DE��(n��1)k��
BH��BN-HN��(n-1)k��
�ɹ��ɶ�������EH��2![]() ��k��
��k��
��sinB��![]() ��
��