题目内容
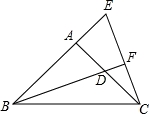
.如图,在△ABC中,∠BAC=90°,AB=AC,D在AC上,过C作CE⊥BD的延长线于F,交BA的延长线于E.
(1)BD与CE相等吗?请说明理由;
(2)BE与AC+AD相等吗?请说明理由.
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)利用已知条件证明△ABD≌△ACE,利用全等三角形的对应边相等得到BD=CE.
(2)由(1)知△ABD≌△ACE,得到AD=AE,由BE=AB+AE,利用线段的等量代换,即可解答.
【解答】解:(1)∵CE⊥BF,
∴∠EFB=90°
∴∠E+∠ABD=90°,
又∵∠BAC=90°,
∴∠EAC=∠BAD=90°
∴∠E+∠ECA=90°,
∴∠ABD=∠ECA,
在△BAD和△ACE中,
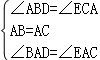 ,
,
∴△ABD≌△ACE,
∴BD=CE.
(2)由(1)知△ABD≌△ACE
∴AD=AE,
又∵AB=AC,
∴AB+AE=AC+AD,
即BE=AC+AD.
【点评】本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△ABD≌△ACE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B. C.
C. D.
D.
 ,
, ,
, ,
, 中,最简分式有( )
中,最简分式有( )
 A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得
A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得
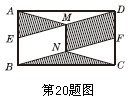
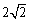 ,BC=
,BC= 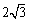 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 .