Question

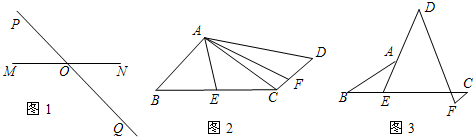
自我操作：如图1所示，点O为线段MN的中点，直线PQ与MN相交于点O，利用此图，作一对以点O为对称中心的全等△MOA和△NOB，并使A、B两点都在直线PQ上。（只保留作图痕迹，不写作法）

（1）探究1：如图2所示，在四边形ABCD中，AB∥CD，点E为BC的中点，∠BAE=∠EAF，AF与DC相交于点F，试探究线段AB与AF，CF之间的等量关系，并证明你的结论；
（2）探究2：如图3所示，DE，BC相交于点E，BA交DE于点A，且BE：EC=1：2，∠BAE=∠EDF，CF∥AB。试探究线段AB与DF，CF之间的等量关系，并证明你的结论；
（3）发现：如图3所示，DE，BC相交于点E，BA交DE于点A，且BE：EC=1：n，∠BAE=∠EDF，CF∥AB。则线段AB与DF，CF之间的等量关系为_____。

Answer 1

解：探究1：AB=AF-CF；
延长AE、DF相交于点M
∵AB∥CD，
∴∠BAE=∠M，∠B=ECM，
又因为BE=CE，
∴△AEB≌△CEM，所以AB=CM，
又因为∠BAE=∠EAF，
∴∠M=∠EAF，
∴MF=AF，
∴AB=CM=FM-CF=AF-CF；
探究2：分别延长DE，CF交于点G，
∵CF∥AB，
∴∠B=∠C，∠BAE=∠G，
∴△ABE≌△GCE，
所以，，又∵，所以，即CG=2AB，
又∵∠BAE=∠EDF，
∴∠G=∠EDF，
所以，FG=DF，
∴2AB=GC=FG+CF=DF+CF；
发现：nAB=DF+CF。