题目内容
已知m满足的条件为：代数式2m-
的值与代数式
的值的和等于5；n=
+
，试求mn的值．
| 5m-1 |
| 3 |
| 7-m |
| 2 |
| a |
| |a| |
| |b| |
| b |
分析：根据两个代数式的值的和等于5列出方程求解得到m的值，再根据绝对值的性质讨论求出n的值，然后代入代数式进行计算即可得解．
解答：解：根据题意，2m-
+
=5，
去分母得，12m-2（5m-1）+3（7-m）=30，
去括号得，12m-10m+2+21-3m=30，
移项得，12m-10m-3m=30-2-21，
合并同类项得，-m=7，
系数化为1得，m=-7，
a、b同号时，n=1+1=2或n=-1+（-1）=-2，
a、b异号时，n=0，
所以，当m=-7、n=2时，mn=（-7）×2=-14，
当m=-7，n=-2时，mn=（-7）×（-2）=14，
当m=-7，n=0时，mn=（-7）×0=0，
综上所述，mn的值为-14或14或0．
| 5m-1 |
| 3 |
| 7-m |
| 2 |
去分母得，12m-2（5m-1）+3（7-m）=30，
去括号得，12m-10m+2+21-3m=30，
移项得，12m-10m-3m=30-2-21，
合并同类项得，-m=7，
系数化为1得，m=-7，
a、b同号时，n=1+1=2或n=-1+（-1）=-2，
a、b异号时，n=0，
所以，当m=-7、n=2时，mn=（-7）×2=-14，
当m=-7，n=-2时，mn=（-7）×（-2）=14，
当m=-7，n=0时，mn=（-7）×0=0，
综上所述，mn的值为-14或14或0．
点评：本题考查了解一元一次方程，绝对值的性质，难点在于分情况讨论求解n的值．
练习册系列答案
相关题目
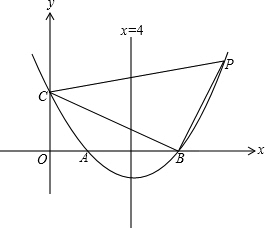点，与y轴交于C点，且A、C坐标为（2，0）、（0，3）．
；
，化简
；
．
；
，化简
；
．