题目内容
(1)计算下列各式并且填空:
1+3= ;
1+3+5= ;
1+3+5+7= ;
1+3+5+7+9= .
(2)细心观察上述运算和结果,计算:1+3+5+…+2001+2003= .
1+3=
1+3+5=
1+3+5+7=
1+3+5+7+9=
(2)细心观察上述运算和结果,计算:1+3+5+…+2001+2003=
分析:(1)根据有理数的加法运算法则分别进行计算即可得解;
(2)根据计算结果,从1开始的连续奇数的和等于首尾两个数的和的一半的平方,然后进行计算即可得解.
(2)根据计算结果,从1开始的连续奇数的和等于首尾两个数的和的一半的平方,然后进行计算即可得解.
解答:解:(1)1+3=4;
1+3+5=9;
1+3+5+7=16;
1+3+5+7+9=25;
(2)1+3+5+…+2001+2003=(
)2=1004004.
故答案为:4,9,16,25;1004004.
1+3+5=9;
1+3+5+7=16;
1+3+5+7+9=25;
(2)1+3+5+…+2001+2003=(
| 1+2003 |
| 2 |
故答案为:4,9,16,25;1004004.
点评:本题是对数字变化规律的考查,观察出计算结果的平方数的底数与首尾两个奇数的关系是解题的关键.

练习册系列答案
相关题目
 =________,②
=________,②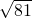 =________,③
=________,③ =________,④
=________,④ =________,通过上述各式,你能发现什么样的规律,用自己的语言叙述出来________.
=________,通过上述各式,你能发现什么样的规律,用自己的语言叙述出来________.