题目内容
正△ABC的边长为12cm，则它的外接圆的半径为
- A.
- B.
- C.
- D.
D
分析：经过圆心O作圆的内接正n边形的一边AB的垂线OC，垂足是C．连接OA，则在直角△OAC中，∠O=180°÷n．OC是边心距r，OA即半径R．AB=2AC=a．根据三角函数即可求解．
解答：连接中心和顶点，作出边心距．
那么得到直角三角形在中心的度数为：360÷3÷2=60°，那么外接圆半径是12÷2÷sin60°=4
．
故选D．
点评：考查了正多边形和圆，做正多边形和圆的问题时，应连接圆心和正多边形的顶点，作出边心距，得到和中心角一半有关的直角三角形进行求解．
分析：经过圆心O作圆的内接正n边形的一边AB的垂线OC，垂足是C．连接OA，则在直角△OAC中，∠O=180°÷n．OC是边心距r，OA即半径R．AB=2AC=a．根据三角函数即可求解．
解答：连接中心和顶点，作出边心距．
那么得到直角三角形在中心的度数为：360÷3÷2=60°，那么外接圆半径是12÷2÷sin60°=4
．故选D．
点评：考查了正多边形和圆，做正多边形和圆的问题时，应连接圆心和正多边形的顶点，作出边心距，得到和中心角一半有关的直角三角形进行求解．
练习册系列答案
相关题目
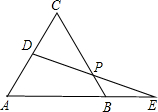
正△ABC的边长为1，P在AB上，PQ⊥BC，QR⊥AC，RS⊥AB．其中Q、R、S为垂足，若SP=
，则AP的长是（ ）
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
交BC于点P．
正△ABC的边长为3cm，边长为1cm的正△RPQ的顶点R与点A重合，点P，Q分别在AC，AB上，将△RPQ沿着边AB，BC，CA逆时针连续翻转（如图所示），直至点P第一次回到原来的位置，则点P运动路径的长为
（2012•内江）如图，正△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C的方向运动，到达点C时停止，设运动时间为x（秒），y=PC2，则y关于x的函数的图象大致为（ ）
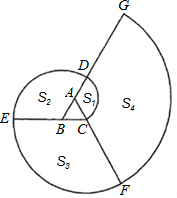依次为A、B、C…．当渐开线延伸开时，形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1．