题目内容
 (2012•内江)如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致为( )
(2012•内江)如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致为( )分析:需要分类讨论:①当0≤x≤3,即点P在线段AB上时,根据余弦定理知cosA=
,所以将相关线段的长度代入该等式,即可求得y与x的函数关系式,然后根据函数关系式确定该函数的图象.②当3<x≤6,即点P在线段BC上时,y与x的函数关系式是y=(6-x)2=(x-6)2(3<x≤6),根据该函数关系式可以确定该函数的图象.
| AP2+AC2-PC2 |
| 2PA•AC |
解答:解:∵正△ABC的边长为3cm,
∴∠A=∠B=∠C=60°,AC=3cm.
①当0≤x≤3时,即点P在线段AB上时,AP=xcm(0≤x≤3);
根据余弦定理知cosA=
,
即
=
,
解得,y=x2-3x+9(0≤x≤3);
该函数图象是开口向上的抛物线;
②当3<x≤6时,即点P在线段BC上时,PC=(6-x)cm(3<x≤6);
则y=(6-x)2=(x-6)2(3<x≤6),
∴该函数的图象是在3<x≤6上的抛物线;
故选C.
∴∠A=∠B=∠C=60°,AC=3cm.
①当0≤x≤3时,即点P在线段AB上时,AP=xcm(0≤x≤3);
根据余弦定理知cosA=
| AP2+AC2-PC2 |
| 2PA•AC |
即
| 1 |
| 2 |
| x2+9-y |
| 6x |
解得,y=x2-3x+9(0≤x≤3);
该函数图象是开口向上的抛物线;
②当3<x≤6时,即点P在线段BC上时,PC=(6-x)cm(3<x≤6);
则y=(6-x)2=(x-6)2(3<x≤6),
∴该函数的图象是在3<x≤6上的抛物线;
故选C.
点评:本题考查了动点问题的函数图象.解答该题时,需要对点P的位置进行分类讨论,以防错选.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (2012•内江)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
(2012•内江)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )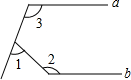 (2012•内江)如图,a∥b,∠1=65°,∠2=140°,则∠3=( )
(2012•内江)如图,a∥b,∠1=65°,∠2=140°,则∠3=( ) (2012•内江)如图所示,A、B是边长为1的小正方形组成的网格的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是
(2012•内江)如图所示,A、B是边长为1的小正方形组成的网格的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是 (2012•内江)如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD=
(2012•内江)如图,四边形ABCD是梯形,BD=AC且BD⊥AC,若AB=2,CD=4,则S梯形ABCD= (2012•内江)如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.
(2012•内江)如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.