题目内容
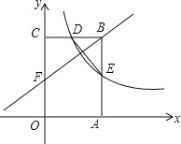
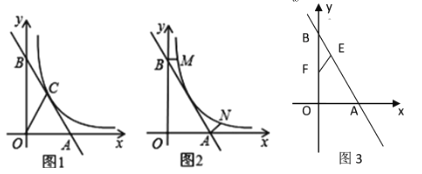
【题目】如图1,一次函数y=2x+4的图象交x轴于点A,交y轴于点B,与反比例函数y=
(x>0)的图象交于点C,连OC,若S△AOC=2.
（1）求反比例函数的解析式；
（2）如图3，点E， F分别是线段AB和线段OB上的动点，点E从点B出发，沿线段BA运动，点F从点O出发，沿线段OB运动，速度都是每秒1个单位长度。运动时间为t秒，当其中一点到达终点后，另一点也随之停止运动.是否存在某个时刻。使得△BEF是直角三角形？若存在，求出t的值若不存在，请说明理由：
（3）如图2，过点B作BM⊥OB交反比例函数y= (x>0)的图象于点M，点N为反比例函数 y= (x>0)的图象上一点，∠ABM =∠BAN，求直线AN的解析式，
【答案】（1）y=
（2）存在某个时刻，使得△BEF是直角三角形，此时t=20-8
或8-16 （3）y=
【解析】
（1）先由一次函数的解析式为y=-2x+4及x轴、y轴上点的坐标特征，求出A（2，0），B（0，4），再根据S△AOC=2，利用三角形的面积公式求出C（1，2），然后运用待定系数法即可求出反比例函数的解析式；
(2)根据题意可得：OF=t，BF＝4-t，BE=t，当△BEF是直角三角形时，有两种情况，∠BFE=90
或∠BEF＝90，再根据两角相等证明△BEF与△BOA相似，列方程即可求出t的值
（3）由A（2，0），B（0，4），C（1，2）三点的坐标，可知C为AB的中点，如图2，延长BM交AN的延长线于D，根据等角对等边得到DB=DA，再连结DC，由等腰三角形三线合一的性质得出DC⊥BA，则∠DCB=∠BOA=90°，由平行线的性质易得∠DBA=∠BAO，那么△DBC∽△BAO，得出DB：BC=BA：AO，求出DB=5，得到D（5，4），然后运用待定系数法即可求出直线AN的解析式；
：
（1）∵一次函数y=-2x+4的图象交x轴于点A，交y轴于点B，
∴A（2，0），B（0，4）．
设C（m，n）．
∵S△AOC=2，
∴
×2×n=2，
解得n=2．
又n=-2m+4，
∴m=1，
∴C（1，2），
所以反比例函数的解析式为y=；
（2）根据题意可得：OF=t，BF＝4-t，BE=t，（0
）
在Rt△ABO中，∵A（2，0），B（0，4）则AB==2
当△BEF是直角三角形时，有两种情况，
①当∠BFE=90
时，
∴∠BFE＝∠AOB ∵∠EBF＝∠ABO
∴△BEF
△BAO
∴
∴
∴t=20-8
②当∠BEF＝90时
同理可得△BEF△BOA
∴
∴
∴t=8-16
综上所述，存在某个时刻，使得△BEF是直角三角形，此时t=20-8
或8-16
（3）∵A（2，0），B（0，4），C（1，2），
∴C为AB的中点，AO=2，BO=4，AB=2，
∴BC=．
如图2，延长BM交AN的延长线于D，
∵∠ABM=∠BAN，
∴DB=DA，
连结DC，则DC⊥BA，
∵BM⊥OB，
∴BM∥OA，
∴∠DBA=∠BAO，
又∠DCB=∠BOA=90°，
∴△DBC∽△BAO，
∴DB：BC=BA：AO，
∴DB=5，
∴D（5，4）．
设直线AN的解析式为y=mx+b，
∵直线AN过A（2，0）、D（5，4），
∴
，解得
∴直线AN的解析式为y=；
