题目内容
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线 交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值是 .
交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值是 .
【答案】分析:设C(x,y),BC=a.过D点作DE⊥OA于E点.
根据DE∥AB得比例线段表示点D坐标;根据△OBC的面积等于3得关系式,列方程组求解.
解答: 解:设C(x,y),BC=a.
解:设C(x,y),BC=a.
则AB=y,OA=x+a.
过D点作DE⊥OA于E点.
∵OD:DB=1:2,DE∥AB,
∴△ODE∽△OBA,相似比为OD:OB=1:3,
∴DE= AB=
AB= y,OE=
y,OE= OA=
OA= (x+a).
(x+a).
∵D点在反比例函数的图象上,且D( (x+a),
(x+a), y),
y),
∴ y•
y• (x+a)=k,即xy+ya=9k,
(x+a)=k,即xy+ya=9k,
∵C点在反比例函数的图象上,则xy=k,
∴ya=8k.
∵△OBC的面积等于3,
∴ ya=3,即ya=6.
ya=3,即ya=6.
∴8k=6,k= .
.
故答案为: .
.
点评:此题考查了反比例函数的应用、平行线分线段成比例及有关图形面积的综合运用,综合性较强.
根据DE∥AB得比例线段表示点D坐标;根据△OBC的面积等于3得关系式,列方程组求解.
解答:
 解:设C(x,y),BC=a.
解:设C(x,y),BC=a.则AB=y,OA=x+a.
过D点作DE⊥OA于E点.
∵OD:DB=1:2,DE∥AB,
∴△ODE∽△OBA,相似比为OD:OB=1:3,
∴DE=
 AB=
AB= y,OE=
y,OE= OA=
OA= (x+a).
(x+a).∵D点在反比例函数的图象上,且D(
 (x+a),
(x+a), y),
y),∴
 y•
y• (x+a)=k,即xy+ya=9k,
(x+a)=k,即xy+ya=9k,∵C点在反比例函数的图象上,则xy=k,
∴ya=8k.
∵△OBC的面积等于3,
∴
 ya=3,即ya=6.
ya=3,即ya=6.∴8k=6,k=
 .
.故答案为:
 .
.点评:此题考查了反比例函数的应用、平行线分线段成比例及有关图形面积的综合运用,综合性较强.

练习册系列答案
相关题目
 9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
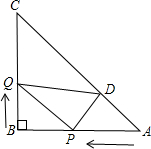 点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.
点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s. (2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为
(2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为