题目内容
阅读理解

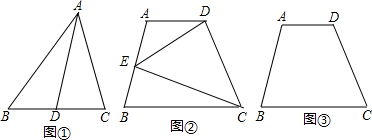
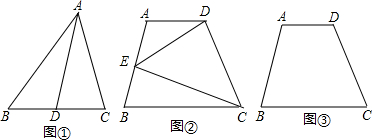
(1)如图①,△ABC中,D是BC中点,连接AD,直接回答S△ABD与S△ADC相等吗?
应用拓展
(2)如图②,已知梯形ABCD中,AD∥BC,E是AB的中点,连接DE、EC,试利用上题得到的结论说明S△DEC=S△ADE+S△EBC;
解决问题
(3)现有一块如图③所示的梯形试验田,想种两种农作物做对比实验,用一条过D点的直线,将这块试验田分割成面积相等的两块,画出这条直线,并简单说明另一点的位置.

(1)如图①,△ABC中,D是BC中点,连接AD,直接回答S△ABD与S△ADC相等吗?
相等
相等
(S表示面积);应用拓展
(2)如图②,已知梯形ABCD中,AD∥BC,E是AB的中点,连接DE、EC,试利用上题得到的结论说明S△DEC=S△ADE+S△EBC;
解决问题
(3)现有一块如图③所示的梯形试验田,想种两种农作物做对比实验,用一条过D点的直线,将这块试验田分割成面积相等的两块,画出这条直线,并简单说明另一点的位置.
分析:(1)由于△ABD与△ACD等底同高,根据三角形的面积公式即可得出S△ABD与S△ADC相等;
(2)延长DE交CB的延长线于点F,根据AAS证明△DAE≌△FBE,则DE=FE,S△DAE=S△FBE,又由(1)的结论可得S△DEC=S△FEC,代入即可说明S△DEC=S△ADE+S△EBC;
(3)取AB的中点E,连接DE并延长,交CB的延长线于点F,则S梯形ABCD=S△CDF,再取CF的中点G,作直线DG,则S△CDG=S△FDG=S梯形ADGB=
S梯形ABCD,故直线DG即可将这块试验田分割成面积相等的两块.
(2)延长DE交CB的延长线于点F,根据AAS证明△DAE≌△FBE,则DE=FE,S△DAE=S△FBE,又由(1)的结论可得S△DEC=S△FEC,代入即可说明S△DEC=S△ADE+S△EBC;
(3)取AB的中点E,连接DE并延长,交CB的延长线于点F,则S梯形ABCD=S△CDF,再取CF的中点G,作直线DG,则S△CDG=S△FDG=S梯形ADGB=
| 1 |
| 2 |
解答: 解:(1)如图①,过点A作AE⊥BC于E.
解:(1)如图①,过点A作AE⊥BC于E.
∵D是BC中点,
∴BD=CD,
又∵S△ABD=
•BD•AE,S△ADC=
•CD•AE,
∴S△ABD=S△ADC.
故答案为相等;
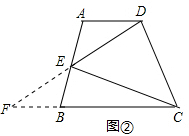 (2)如图②,延长DE交CB的延长线于点F.
(2)如图②,延长DE交CB的延长线于点F.
∵E是AB的中点,∴AE=BE.
∵AD∥BC,∴∠ADE=∠BFE.
在△DAE与△FBE中,
,
∴△DAE≌△FBE(AAS),
∴DE=FE,S△DAE=S△FBE,
∴E是DF中点,
 ∴S△DEC=S△FEC=S△BFE+S△EBC=S△ADE+S△EBC,
∴S△DEC=S△FEC=S△BFE+S△EBC=S△ADE+S△EBC,
∴S△DEC=S△ADE+S△EBC;
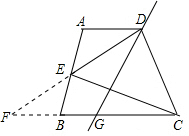
(3)如图所示:
取AB的中点E,连接DE并延长,交CB的延长线于点F,取CF的中点G,作直线DG,
则直线DG即可将这块试验田分割成面积相等的两块.
 解:(1)如图①,过点A作AE⊥BC于E.
解:(1)如图①,过点A作AE⊥BC于E.∵D是BC中点,
∴BD=CD,
又∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABD=S△ADC.
故答案为相等;
 (2)如图②,延长DE交CB的延长线于点F.
(2)如图②,延长DE交CB的延长线于点F.∵E是AB的中点,∴AE=BE.
∵AD∥BC,∴∠ADE=∠BFE.
在△DAE与△FBE中,
|
∴△DAE≌△FBE(AAS),
∴DE=FE,S△DAE=S△FBE,
∴E是DF中点,
 ∴S△DEC=S△FEC=S△BFE+S△EBC=S△ADE+S△EBC,
∴S△DEC=S△FEC=S△BFE+S△EBC=S△ADE+S△EBC,∴S△DEC=S△ADE+S△EBC;
(3)如图所示:
取AB的中点E,连接DE并延长,交CB的延长线于点F,取CF的中点G,作直线DG,
则直线DG即可将这块试验田分割成面积相等的两块.
点评:本题考查了三角形的面积,全等三角形的判定与性质,梯形的性质,作图-应用与设计作图,(2)中通过作辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目

 BC。
BC。 