题目内容
设△A1B1C1的面积是S1,△A2B2C2的面积为S2(S1<S2),当△A1B1C1∽△A2B2C2,且0.3≤| S1 | S2 |
(1)若AD=DC,求证:△DAC与△ABC有一定的“全等度”;
(2)你认为:△DAC与△ABC有一定的“全等度”正确吗?若正确,说明理由;若不正确,请举出一个反例说明.

分析:(1)先过点D作DE⊥AC,交AC于E,利用AD∥BC,AD=DC,∠BCD=60°,可证∠DAC=∠ACD=∠ACB=30°,那么△ABC和△DAC中就有两组对应角相等,即可求它们相似.可以设DE=x,由于∠DAC=30°,所以AD=2x,AE=
x,那么利用等腰三角形三线合一定理,可知AC=2
x=AB,于是S△DAC:S△ABC=DA:AB=(
)2=1:3,而0.3≤
≤0.4,所以两三角形有一定的全等度;
(2)不正确,举出反例进行论证其错误即可.比如可令∠ACB=40°,则∠ACD=20°,∠DAC=40°,∠BAC=110°,∠ADC=120°,显然两个三角形不相似,当然就不存在全等度了.
| 3 |
| 3 |
| 2x | ||
2
|
| 1 |
| 3 |
(2)不正确,举出反例进行论证其错误即可.比如可令∠ACB=40°,则∠ACD=20°,∠DAC=40°,∠BAC=110°,∠ADC=120°,显然两个三角形不相似,当然就不存在全等度了.
解答: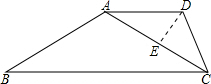 (1)证明:∵AD=DC
(1)证明:∵AD=DC
∴∠DAC=∠DCA
∵AD∥BC
∴∠DAC=∠ACB
∵∠BCD=60°
∴∠ACD=∠ACB=30°
∵∠B=30°
∴∠DAC=∠B=30°
∴△DAC∽△ABC
过点D作DE⊥AC于点E,
∵AD=DC
∴AC=2EC
在Rt△DEC中
∵∠DCA=30°,cos∠DCA=
=
∴DC=
EC
∴
=
∴
=(
)2=
≈0.33,
∵0.3≤
≤0.4
∴△DAC与△ABC有一定的“全等度”.
(2)解:△DAC与△ABC有一定的△“全等度”不正确.
反例:若
∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”.
∵∠B=30°,∠BCD=60°,
∴∠BAC=110°
∵AD∥BC
∴∠D=120°
∴△DAC与△ABC不相似
∴若∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”.
 (1)证明:∵AD=DC
(1)证明:∵AD=DC∴∠DAC=∠DCA
∵AD∥BC
∴∠DAC=∠ACB
∵∠BCD=60°
∴∠ACD=∠ACB=30°
∵∠B=30°
∴∠DAC=∠B=30°
∴△DAC∽△ABC
过点D作DE⊥AC于点E,
∵AD=DC
∴AC=2EC
在Rt△DEC中
∵∠DCA=30°,cos∠DCA=
| EC |
| DC |
| ||
| 2 |
∴DC=
| 2 | ||
|
∴
| DC |
| AC |
| 1 | ||
|
∴
| S△DAC |
| S△ABC |
| DC |
| AC |
| 1 |
| 3 |
∵0.3≤
| S△DEC |
| S△ADC |
∴△DAC与△ABC有一定的“全等度”.
(2)解:△DAC与△ABC有一定的△“全等度”不正确.
反例:若
∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”.
∵∠B=30°,∠BCD=60°,
∴∠BAC=110°
∵AD∥BC
∴∠D=120°
∴△DAC与△ABC不相似
∴若∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”.
点评:本题利用了等边对等角的性质、平行线的性质、三角函数值、相似三角形的判定、相似三角形的面积比等于相似比的平方等知识.

练习册系列答案
相关题目
 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
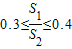 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.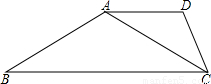
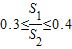 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.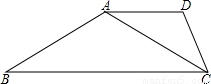
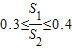 时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.
时,则称△A1B1C1与△A2B2C2有一定的“全等度”.如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC.