题目内容
(1)如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
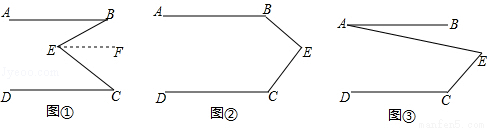
证明过程如下:
证明:过点E作EF∥AB,
∵AB∥DC,EF∥AB(辅助线的作法),
∴EF∥DC
∴∠C=∠CEF.
∵EF∥AB,∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC.
(2)如果点E运动到图②所示的位置,其他条件不变,∠B,∠C,∠BEC又有什么关系?并证明你的结论;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(写出结论,不用写计算过程)。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数 | 中位数 | 众数 | 方差 |
8.5 | 8.3 | 8.1 | 0.15 |
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A. 平均数 B. 众数 C. 方差 D. 中位数


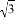 ,PA=
,PA=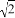 ,则:
,则: ,求
,求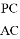 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求) 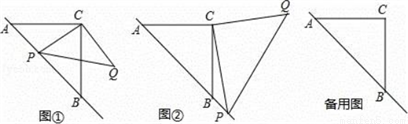
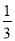 AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB=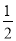 S△ABC.其中正确的结论是_______________(只填番号)
S△ABC.其中正确的结论是_______________(只填番号)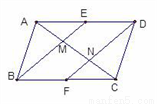
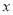 的值
的值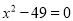 ; (3) 8
; (3) 8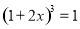
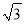 ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.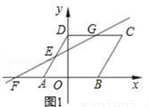
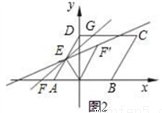
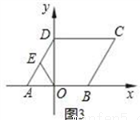
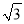 .
.