Question

【题目】（8分）如图，在△ABC中，∠ABC=45，CD⊥AB，BE⊥AC，垂足分别为D、E，F为BC中点，BE与DF、DC分别交于点G、H，∠ABE=∠CBE。

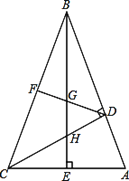
（1）线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；

（2）求证：

Answer 1

【答案】（1）BH=AC,（2）证明见解析.

【解析】试题分析：（1）由CD⊥AB知∠BDC=∠BEC，因为∠ABC=45，所以∠ABC=∠BCD ，故CD="BD" 又因BE⊥AC所以∠ACD,∠ABE都是∠A的余角故相等，因此可证△DBH≌△DCA所以BH=AC

（2） 连接GC，根据“等腰三角形三线合一”的性质：由BE⊥AC，∠ABE=∠CBE可得AE=CE

BF=FC,BD=CD得BG=CG因为GC2-GE2=CE2.所以BG2-GE2=EA2

试题解析：（1）BH="AC"

证明：∵∠BDC=∠BEC=∠CDA=90, ∠ABC=45,

∴∠BCD=45=∠ABC,

∴DB=DC.

又∵∠BHD=∠CHE

∴∠DBH=∠DCA

∴△DBH≌△DCA

∴BH=AC.

（2）证明：连接GC，∴GC2-GE2=CE2.

∵F为BC的中点，DB=DC

∴DF垂直平分BC，

∴BG=GC，∴BG2-GE2=EC2

∵∠ABE=∠CBE ∴EC="EA"

∴BG2-GE2=EA2