Question

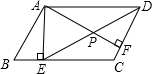如图所示，在平行四边形ABCD中，AE⊥BC于点E，AF⊥CD于点F，∠ADC=60°，BE=2，CF=1，连接DE交AF于点P，那么PE的长为________．

Answer 1

分析：根据平行四边形的性质，可求出∠B，运用勾股定理可求出AE=2，再进一步求出DE，证明△AEP是等边三角形，所以可求出PE．
解答：由题意得∠B=∠ADC=60°
在Rt△ABE中：∵BE=2
∴AB=4
∴AE=2．
∴CD=4，
∵CF=1
∴DF=CD-CF=3
在Rt△AFD中：∵FD=3
∴AD=6
在Rt△AED中：∵AE=2，AD=6
∴ED=4，
∴∠AED=60°
∵∠BAD=120°，∠BAE=30°，∠FAD=30°
∴∠EAP=60°
∴△AEP是等边三角形
∴PE=AE=2．
故答案为2．
点评：解决本题的关键是利用勾股定理等知识点得到所求线段相关的三角形的形状以及相应线段的值．