题目内容
 如图,直线y=kx+b与反比例函数y=
如图,直线y=kx+b与反比例函数y=| k | x |
(1)试确定反比例函数的关系式;
(2)求一次函数的关系式;
(3)求△AOC的面积.
分析:(1)直接把A点坐标(-2,4)代入y=
可求出k的值,从而确定反比例函数解析式;
(2)由A(-2,4)和B(-4,2),利用待定系数法可确定一次函数的解析式;
(3)先利用直线解析式确定C点坐标,然后利用三角形面积公式计算△AOC的面积.
| k |
| x |
(2)由A(-2,4)和B(-4,2),利用待定系数法可确定一次函数的解析式;
(3)先利用直线解析式确定C点坐标,然后利用三角形面积公式计算△AOC的面积.
解答:解:(1)把A(-2,4)代入y=
得k=-2×4=-8,
所以反比例函数解析式为y=-
;
(2)把x=-4代入y=-
得y=2,
所以B点坐标为(-4,2),
把A(-2,4)和B(-4,2)代入y=kx+b得
,解方程组得
,
所以一次函数的解析式为y=x+6;
(3)对y=x+6,令y=0,则x+6=0,解得x=-6,
所以C点坐标为(-6,0),
所以S△AOC=
×6×4=12.
| k |
| x |
所以反比例函数解析式为y=-
| 8 |
| x |
(2)把x=-4代入y=-
| 8 |
| x |
所以B点坐标为(-4,2),
把A(-2,4)和B(-4,2)代入y=kx+b得
|
|
所以一次函数的解析式为y=x+6;
(3)对y=x+6,令y=0,则x+6=0,解得x=-6,
所以C点坐标为(-6,0),
所以S△AOC=
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了观察函数图象的能力以及用待定系数法确定一次函数的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
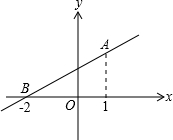 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为