题目内容
1.下列命题:①相似三角形一定不是全等三角形;②相似三角形对应中线的比等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O是△ABC内任意一点,OA、OB、OC的中点连成的三角形△A′B′C′∽△ABC.其中正确的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据全等三角形的定义:全等三角形就是能重合的三角形,形状相同,大小相同;相似三角形的定义:相似三角形是形状相同的三角形,大小不一定相等;相似多边形的定义:相似多边形就是形状相同的多边形,根据这些定义逐一分析解答即可.
解答 解:①、相似三角形是形状相同的三角形,大小不一定相同,全等三角形就是能重合的三角形,形状相同,大小相同,因而全等三角形是特殊的相似三角形,此选项错误;
②、相似三角形对应中线的比、对应角平分线的比都等于相似比,此选项正确;
③、边数相同,对应角分别相等的两个矩形不一定相似,此选项错误;
④、根据三角形的中位线得出三条边对应的比值为$\frac{1}{2}$,两个三角形相似,此选项正确.
故正确的命题是:②④共2个.
故选:C.
点评 此题考查命题与定理,掌握三角形全等与相似之间的联系,相似的判定,中位线定理是解决问题的关键.

练习册系列答案
相关题目
16.二次函数y=ax2+bx+c的图象上部分点的对应值如下表:
则关于x的一元二次方程ax2+bx+c=0(a≠0)的解为-1或2.
| x | … | -2 | -1 | 0 | 1 | … |
| y | … | 4 | 0 | -2 | -2 | … |
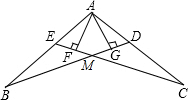 如图,AB=AC,点D、E分别在AC、AB上,AG⊥BD于点G,AF⊥CE于点F,且AE=AD,EF=DG.求证:BG=CF.
如图,AB=AC,点D、E分别在AC、AB上,AG⊥BD于点G,AF⊥CE于点F,且AE=AD,EF=DG.求证:BG=CF.