题目内容
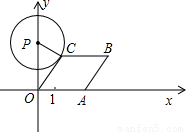
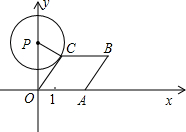
 如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=________.
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=________.
 或
或 或
或
分析:⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=
 ,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
,表示出OC,等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.解答:分三种情况考虑:
①当⊙P与OC相切时(如图1),切点为C,此时PC⊥OC,
 ∵OA=1+t,四边形OABC为菱形,
∵OA=1+t,四边形OABC为菱形,∴OC=1+t,
∴OC=OPcos30°,
∴1+t=3•
 ,
,∴t=
 -1;
-1;②当⊙P与OA,即与x轴相切时(如图2),
 切点为O,PC=OP=3,
切点为O,PC=OP=3,过P作PE⊥OC于E,则OE=
 OC,
OC,∴
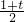 =OPcos30°=
=OPcos30°= ,
,∴t=3
 -1;
-1;③当⊙P与AB所在直线相切时(如图3),
设切点为F,PF交OC于G,则PF⊥OC,

∴FG=CD=(1+t)sin60°=
 (1+t),
(1+t),∴PC=PF=OPsin30°+
 (1+t)=
(1+t)= +
+ (1+t),
(1+t),过C作CH⊥y轴于H,
在Rt△PHC中,利用勾股定理得:PH2+CH2=PC2,
∴(
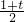 )2+(
)2+( -3)2=(
-3)2=( +
+ )2,
)2,化简得:(t+1)2-18
 (t+1)+27=0,
(t+1)+27=0,解得:t+1=9
 ±6
±6 ,
,∵t=9
 -6
-6 -1<0,
-1<0,∴t=9
 +6
+6 -1,
-1,∴所求t的值为
 -1或3
-1或3 -1或9
-1或9 +6
+6 -1.
-1.故答案为:
 -1或3
-1或3 -1或9
-1或9 +6
+6 -1.
-1.点评:此题考查了切线的性质,菱形的性质,特殊角的三角函数值,及勾股定理的运用,利用了分类讨论的思想,熟练掌握切线的性质是解本题的关键,同时注意锐角三角函数定义及特殊角的三角函数值的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求: ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由. ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.