题目内容
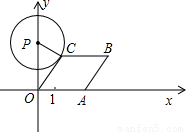
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,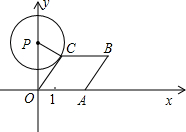 A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:(1)点C的坐标(用含t的代数式表示);
(2)当点A在运动过程中,所有使⊙P与菱形OABC的边所在直线相切的t的值.
分析:(1)过C向x轴引垂线,利用三角函数求出相应的横纵坐标;
(2)⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分情况探讨.
(2)⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分情况探讨.
解答: 解:(1)过C作CD⊥x轴于D.
解:(1)过C作CD⊥x轴于D.
∵OA=1+t,
∴OC=1+t,
∴OD=OCcos60°=
,DC=OCsin60°=
.
∴点C的坐标为(
,
).
(2)①当⊙P与OC相切时(如图1),切点为C,此时PC⊥OC.
∴OC=OPcos30°,
∴1+t=3•
,
∴t=
-1.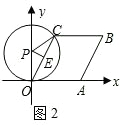
②当⊙P与OA,即与x轴相切时(如图2),则切点为O,PC=OP.
过P作PE⊥OC于E,则OE=
OC.
∴
=OPcos30°=
,
∴t=3
-1.
③当⊙P与AB所在直线相切时(如图3),设切点为F,PF交OC于G,则PF⊥OC.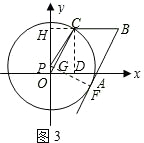
∴FG=CD=
,
∴PC=PF=OPsin30°+
.
过C作CH⊥y轴于H,则PH2+CH2=PC2.
∴(
)2+(
-3)2=(
+
)2,
化简,得(t+1)2-18
(t+1)+27=0,
解得t+1=9
±6
.
∵t=9
-6
-1<0,
∴t=9
+6
-1.
∴所求t的值是
-1,3
-1和9
+6
-1.
 解:(1)过C作CD⊥x轴于D.
解:(1)过C作CD⊥x轴于D.∵OA=1+t,
∴OC=1+t,
∴OD=OCcos60°=
| 1+t |
| 2 |
| ||
| 2 |
∴点C的坐标为(
| 1+t |
| 2 |
| ||
| 2 |
(2)①当⊙P与OC相切时(如图1),切点为C,此时PC⊥OC.
∴OC=OPcos30°,
∴1+t=3•
| ||
| 2 |
∴t=
3
| ||
| 2 |

②当⊙P与OA,即与x轴相切时(如图2),则切点为O,PC=OP.
过P作PE⊥OC于E,则OE=
| 1 |
| 2 |
∴
| 1+t |
| 2 |
3
| ||
| 2 |
∴t=3
| 3 |
③当⊙P与AB所在直线相切时(如图3),设切点为F,PF交OC于G,则PF⊥OC.

∴FG=CD=
| ||
| 2 |
∴PC=PF=OPsin30°+
| ||
| 2 |
过C作CH⊥y轴于H,则PH2+CH2=PC2.
∴(
| 1+t |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
化简,得(t+1)2-18
| 3 |
解得t+1=9
| 3 |
| 6 |
∵t=9
| 3 |
| 6 |
∴t=9
| 3 |
| 6 |
∴所求t的值是
3
| ||
| 2 |
| 3 |
| 3 |
| 6 |
点评:四边形所在的直线和圆相切,那么与各边都有可能相切;
注意特殊三角函数以及勾股定理的应用.
注意特殊三角函数以及勾股定理的应用.

练习册系列答案
相关题目
 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由. ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.