题目内容
已知关于 的一元二次方程
的一元二次方程 2-
2-
 -2=0①.
-2=0①.
(1)若 =-1是方程①的一个根,求
=-1是方程①的一个根,求 的值和方程①的另一根;
的值和方程①的另一根;
(2)对于任意实数 ,判断方程①的根的情况,并说明理由.
,判断方程①的根的情况,并说明理由.
(1)m=1,另一根是2;(2)方程①有两个不相等的实数根.
解析试题分析:(1)直接把x=-1代入方程即可求得m的值,然后解方程即可求得方程的另一个根;
(2)利用一元二次方程根的情况可以转化为判别式△与0的关系进行判断.
(1)把x=-1代入得1+m-2=0,解得m=1
∴ 2-
2- -2=0.
-2=0.
∴
∴另一根是2;
(2)∵ ,
,
∴方程①有两个不相等的实数根.
考点:本题考查的是根的判别式,一元二次方程的解的定义,解一元二次方程
点评:解答本题的关键是熟练掌握一元二次方程根的情况与判别式△的关系:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程  的一元二次方程
的一元二次方程 的两个整数根恰好比方程
的两个整数根恰好比方程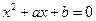 的两个根都大1,求
的两个根都大1,求 的值.
的值.  的一元二次方程x2+2x+m=0.
的一元二次方程x2+2x+m=0. 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根. 的取值范围;
的取值范围;