题目内容
【题目】如图①,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向终点
边向终点![]() 以每秒
以每秒![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向终点
边向终点![]() 以每秒
以每秒![]() 的速度移动,当其中一点到达终点时运动停止,设运动时间为
的速度移动,当其中一点到达终点时运动停止,设运动时间为![]() 秒.
秒.
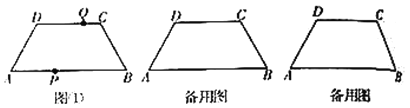
(1)求证:当![]() 时,四边形
时,四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 为何值时,线段
为何值时,线段![]() 平分对角线
平分对角线![]() ?并求出此时四边形
?并求出此时四边形![]() 的周长;
的周长;
(3)当![]() 为何值时,点
为何值时,点![]() 恰好在
恰好在![]() 的垂直平分线上?
的垂直平分线上?
【答案】(1)见解析;(2)t=3, ![]() ;(3)
;(3) ![]() .
.
【解析】
(1)根据![]() ,求出DQ,AP的长,再根据平行四边形的判定定理即可求解;
,求出DQ,AP的长,再根据平行四边形的判定定理即可求解;
(2)根据题意得到DE=BE,根据矩形的性质得到![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,即可求出t的值,再根据勾股定理即可求解;
,即可求出t的值,再根据勾股定理即可求解;
(3)分别过点![]() 、
、![]() 作
作![]() ,
,![]() ,根据矩形的性质可得
,根据矩形的性质可得![]() ,求出
,求出 ![]() 的长,再根据垂直平分线的性质得到PD=PQ,故DE=PM,代入即可求出t的值.
的长,再根据垂直平分线的性质得到PD=PQ,故DE=PM,代入即可求出t的值.
(1)证明:∵![]() ,
,
∴当![]() 秒时,两点停止运动,在运动过程中
秒时,两点停止运动,在运动过程中![]() ,
,![]() ,
,
∴![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
(2)如图①,设![]() 交
交![]() 于点
于点![]() ,若
,若![]() 平分对角线
平分对角线![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,符合题意,
,符合题意,
∴当![]() 秒时,
秒时,![]() 平分对角线
平分对角线![]() ,
,
此时![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
由勾股定理,得![]() ,
,
∴四边形![]() 的周长
的周长![]() .
.
(3)如图②,分别过点![]() 、
、![]() 作
作![]() ,
,![]() ,分别交
,分别交![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,
,
可得四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在
在![]() 的垂直平分线
的垂直平分线![]() 上,
上,
∴![]() ,
,![]() ,四边形
,四边形![]() 是矩形,
是矩形,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
则当![]() 为
为![]() 时,点
时,点![]() 恰好在
恰好在![]() 的垂直平分线上.
的垂直平分线上.


【题目】在6.26国际禁毒日到来之际,某市教委为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛,某校七年级、八年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级 | 68 | 88 | 100 | 100 | 79 | 94 | 89 | 85 | 100 | 88 |
100 | 90 | 98 | 97 | 77 | 94 | 96 | 100 | 92 | 67 | |
八年级 | 69 | 97 | 91 | 69 | 98 | 100 | 99 | 100 | 90 | 100 |
99 | 89 | 97 | 100 | 99 | 94 | 79 | 99 | 98 | 79 |
(1)根据上述数据,将下列表格补充完成.
(整理、描述数据):
分数段 |
|
|
|
|
七年级人数 | 2 | ___________ | ___________ | 12 |
八年级人数 | 2 | 2 | 1 | 15 |
(分析数据):样本数据的平均数、中位数如下表:
年级 | 平均数 | 中位数 |
七年级 | 90.1 | 93 |
八年级 | 92.3 | ___________ |
(得出结论):
(2)你认为哪个年级掌握禁毒知识的总体水平较好,从两个方面说明你的理由.