题目内容
（2013•衡水模拟）已知函数y=（k-3）x2+2x+1的图象与x轴有两个交点，则k的取值范围是
k≤4且k≠3
k≤4且k≠3
．分析：根据题意知，关于x的一元二次方程（k-3）x2+2x+1=0，然后根据一元二次方程的定义和根的判别式来求k的取值范围．
解答：解：∵函数y=（k-3）x2+2x+1的图象与x轴有两个交点，
∴令y=0，则（k-3）x2+2x+1=0，则
△=4-4（k-3）≥0，且k-3≠0，
解得，k≤4且k≠3．
故答案是：k≤4且k≠3．
∴令y=0，则（k-3）x2+2x+1=0，则
△=4-4（k-3）≥0，且k-3≠0，
解得，k≤4且k≠3．
故答案是：k≤4且k≠3．
点评：本题考查了抛物线与x轴的交点．二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系．
△=b2-4ac决定抛物线与x轴的交点个数．
△=b2-4ac＞0时，抛物线与x轴有2个交点；
△=b2-4ac=0时，抛物线与x轴有1个交点；
△=b2-4ac＜0时，抛物线与x轴没有交点．
△=b2-4ac决定抛物线与x轴的交点个数．
△=b2-4ac＞0时，抛物线与x轴有2个交点；
△=b2-4ac=0时，抛物线与x轴有1个交点；
△=b2-4ac＜0时，抛物线与x轴没有交点．
练习册系列答案
相关题目
（2013•衡水模拟）二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象不经过（ ）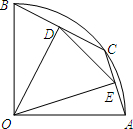
（2013•衡水模拟）如图，在半径为2的扇形AOB中，∠AOB=90°，点C是
