题目内容
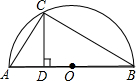 已知AB是半圆O的直径,过⊙O上一点C作CD⊥AB于点D AC=3cm,BC=4cm,则AB=________cm,CD=________cm,tan∠ACD=________.
已知AB是半圆O的直径,过⊙O上一点C作CD⊥AB于点D AC=3cm,BC=4cm,则AB=________cm,CD=________cm,tan∠ACD=________.
5 

分析:根据题意,易得∠ACB=90°.由勾股定理,求AB的长,进而由三角形面积公式,可得CD的值.再根据锐角三角函数的定义计算tan∠ACD的值.
解答:∵AB是半圆O的直径,∴∠ACB=90°.
在Rt△ACB中,AB= =5.
=5.
∵S= ×CD×AB=
×CD×AB= ×AC×BC,
×AC×BC,
∴CD= =
= .
.
由勾股定理可得,AD= ,
,
tan∠ACD=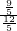 =
= .
.
点评:本题考查直角三角形有关性质的运用,解题时,注意结合三角函数的定义,灵活运用.


分析:根据题意,易得∠ACB=90°.由勾股定理,求AB的长,进而由三角形面积公式,可得CD的值.再根据锐角三角函数的定义计算tan∠ACD的值.
解答:∵AB是半圆O的直径,∴∠ACB=90°.
在Rt△ACB中,AB=
 =5.
=5.∵S=
 ×CD×AB=
×CD×AB= ×AC×BC,
×AC×BC,∴CD=
 =
= .
.由勾股定理可得,AD=
 ,
,tan∠ACD=
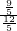 =
= .
.点评:本题考查直角三角形有关性质的运用,解题时,注意结合三角函数的定义,灵活运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
