题目内容
3.若2(a2+3)的值与3(1-a2)的值互为相反数,求$\frac{3+a}{{a}^{2}}$的值.分析 根据相反数得出方程,求出方程的解,最后分别代入求出即可.
解答 解:根据题意得:2(a2+3)+3(1-a2)=0
即a2=9,
解得:a=±3,
当a=3时,$\frac{3+a}{{a}^{2}}$=$\frac{3+3}{{3}^{2}}$=$\frac{2}{3}$;
当a=-3时,$\frac{3+a}{{a}^{2}}$=$\frac{3-3}{{3}^{2}}$=0.
点评 本题考查了相反数,解一元二次方程,求代数式的值的应用,能求出a的值是解此题的关键,注意:互为相反数的两个数的和为0.

练习册系列答案
相关题目
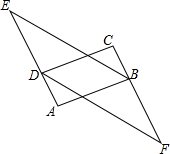 如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.
如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.
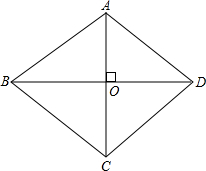 如图,菱形的两条对角线分别是16和12,较长的一条对角线与菱形的一边的夹角为θ,tanθ=$\frac{3}{4}$.
如图,菱形的两条对角线分别是16和12,较长的一条对角线与菱形的一边的夹角为θ,tanθ=$\frac{3}{4}$.