题目内容
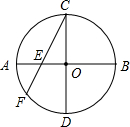 如图所示,AB,CD是半径为5的圆内互相垂直的两条直径,E为AO的中点,连接CE并延长,交⊙O于另一点F,求弦CF的长.
如图所示,AB,CD是半径为5的圆内互相垂直的两条直径,E为AO的中点,连接CE并延长,交⊙O于另一点F,求弦CF的长.分析:首先连接FD,由直径所对的圆周角是直角,可得∠CFD=90°,又由CD⊥AB,易证得△COE∽△CFD,然后由相似三角形的对应边成比例与勾股定理,求得弦CF的长.
解答: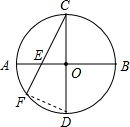 解:连接FD,
解:连接FD,
∵CD是直径,
∴∠CFD=90°,
∵CD⊥AB,
∴∠COE∠CFD=90°,
∵∠ECO=∠DCF,
∴△COE∽△CFD,
∴
=
,
即CF=
,
∵OE=
AO=
×5=2.5,
在Rt△COE中,CE=
=
,
∴CF=
=4
.
 解:连接FD,
解:连接FD,∵CD是直径,
∴∠CFD=90°,
∵CD⊥AB,
∴∠COE∠CFD=90°,
∵∠ECO=∠DCF,
∴△COE∽△CFD,
∴
| CD |
| CF |
| CE |
| CO |
即CF=
| CO•CD |
| CE |
∵OE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△COE中,CE=
| CO2+OE2 |
5
| ||
| 2 |
∴CF=
| 5×10 | ||||
|
| 5 |
点评:此题考查了圆周角定理、相似三角形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图所示,AB、CD相交于点0,连接AC,BD,添加下列一个条件后,仍不能判定△AOC∽△DOB的是( )
如图所示,AB、CD相交于点0,连接AC,BD,添加下列一个条件后,仍不能判定△AOC∽△DOB的是( )| A、∠A=∠D | ||||
B、
| ||||
| C、∠B=∠C | ||||
D、
|
 梯形ABCD如图所示,AB、CD分别为梯形上下底,已知阴影部分总面积为5平方厘米,△AOB的面积是0.625平方厘米.则梯形ABCD的面积是
梯形ABCD如图所示,AB、CD分别为梯形上下底,已知阴影部分总面积为5平方厘米,△AOB的面积是0.625平方厘米.则梯形ABCD的面积是
 14、如图所示,AB、CD相交于点O,OE⊥AB,则∠AOC的对顶角是
14、如图所示,AB、CD相交于点O,OE⊥AB,则∠AOC的对顶角是 如图所示,AB平行CD,AE与CE相交于点E,∠BAE=30°,∠DCE=40°.∠1=
如图所示,AB平行CD,AE与CE相交于点E,∠BAE=30°,∠DCE=40°.∠1=