题目内容
15.阅读材料:善于思考的小军在解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{4x+11y=5②}\end{array}\right.$时,采用了一种“整体代换”的解法:解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5③
把方程①代入③得:2×3+y=5,∴方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组$\left\{\begin{array}{l}{3x-2y=5①}\\{9x-4y=19②}\end{array}\right.$;
(2)已知x,y满足方程组$\left\{\begin{array}{l}{3{x}^{2}-2xy+12{y}^{2}=47①}\\{2{x}^{2}+xy+8{y}^{2}=36②}\end{array}\right.$,求xy的值.
分析 (1)由②变形得:3(3x-2y)+2y=19③,把①代入③得:15+2y=19,即y=2即可;
(2)由②变形化简得x2+4y2=18-$\frac{xy}{2}$③,整体代入即可.
解答 解:(1)由②变形得:3(3x-2y)+2y=19③,
把①代入③得:15+2y=19,即y=2,
把y=2代入①得:x=3,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$;
(2)由②变形得:2(x2+4y2)+xy=36,即:x2+4y2=18-$\frac{xy}{2}$③,
由①变形得:3(x2+4y2)-2xy=47④,
把③代入④得:3×(18-$\frac{xy}{2}$)-2xy=47,
∴xy=2.
点评 此题考查了解二元一次方程组,熟练掌握整体代入是解本题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.某灯泡厂生产节能灯泡1000只,其中有5只是次品,如果从中任取1只,这只灯泡是次品的概率是( )
| A. | $\frac{1}{1000}$ | B. | $\frac{1}{500}$ | C. | $\frac{1}{200}$ | D. | $\frac{95}{1000}$ |
5. 如图所示,已知AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,那么∠ADB等于( )
如图所示,已知AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,那么∠ADB等于( )
 如图所示,已知AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,那么∠ADB等于( )
如图所示,已知AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,那么∠ADB等于( )| A. | 45° | B. | 30° | C. | 50° | D. | 36° |
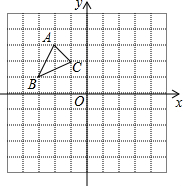 如图,△ABC的顶点分别为:A(-2,3),B(-3,1),C(-1,2).
如图,△ABC的顶点分别为:A(-2,3),B(-3,1),C(-1,2).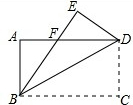 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F.求证:AF=EF.
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F.求证:AF=EF.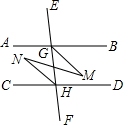 如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.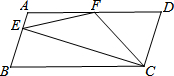 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论: