题目内容
【题目】阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“3倍角三角形”例如：一个三角形三个内角的度数分别是
，这个三角形就是一个“3倍角三角形”．反之，若一个三角形是“3倍角三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍．
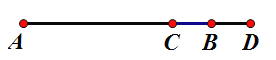
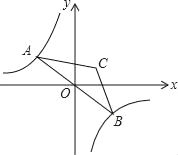
（1）如图1，已知
，在射线
上取一点
，过点作
交
于点
．判断
是否是“3倍角三角形”，为什么？
（2）在（1）的条件下，以为端点画射线
，交线段
于点
（点不与点
、点重合)．若
是“3倍角三角形”，求
的度数．
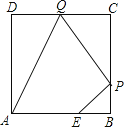
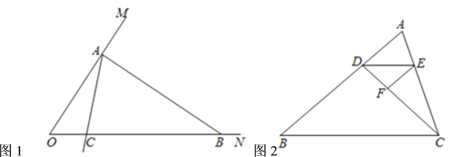
（3）如图2，点
在
的边上，连接
，作
的平分线交
于点
，在上取一点
，使得
，
．若
是“3倍角三角形”，求
的度数．
【答案】（1）是，理由详见解析；（2）
或
；（3）
或
．
【解析】
（1）根据“3倍角三角形”的定义进行判断即可得出答案；
（2）根据“3倍角三角形”的定义，分两种情况：当
时， 当
，
都是“3倍角三角形”，分别进行讨论即可；
（3）根据平行线的性质可得出
，然后利用角平分线的定义有
，根据等量代换有
，再根据
是“3倍角三角形”，则有
或
两种情况，最后根据三角形内角和求出
的度数即可．
解：（1）是，
理由：
，
，
，
，
为“3倍角三角形”．
（2）
当时，是“3倍角三角形”，
此时
当，是“3倍角三角形”
此时
，
；
（3）
，
，
，
，
，
，
，
，
平分
，
，
，
是“3倍角三角形”，
或，
，
或．
练习册系列答案
相关题目
