题目内容
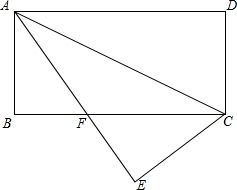如图，矩形ABCD中，AB=6，AD=8，将△ADC沿AC翻折至△AEC，AE与BC相交于F，求FC的长．考点：翻折变换（折叠问题）,矩形的性质
专题：
分析：利用翻折变换的性质得出∠2=∠3，进而利用勾股定理求出FC的长．
解答：
解：如图所示：由题意可得：∠1=∠2，∠1=∠3，
则∠2=∠3，
故AF=FC，设FC=AF=x，则BF=8-x，
在Rt△ABF中
AB2+BF2=AF2，
则62+（8-x）2=x2，
解得：x=
，
故FC=
．
解：如图所示：由题意可得：∠1=∠2，∠1=∠3，则∠2=∠3，
故AF=FC，设FC=AF=x，则BF=8-x，
在Rt△ABF中
AB2+BF2=AF2，
则62+（8-x）2=x2，
解得：x=
| 25 |
| 4 |
故FC=
| 25 |
| 4 |
点评：此题主要考查了翻折变换的性质以及勾股定理等知识，得出AF=FC是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
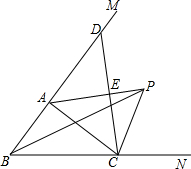如图：△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，连接AP．
为了提高市民的宜居环境，某区规划修建一个文化广场（平面图形如图所示），其中四边形ABCD是长方形，分别以AB、BC、CD、DA边为直径向外作半圆，若整个广场的周长为628米（π取3.14），BC边为97米．
