题目内容
20. 如图,△ABC中,∠B=90°,AB+BC=2+$\sqrt{6}$,AC=2,求△ABC的面积.
如图,△ABC中,∠B=90°,AB+BC=2+$\sqrt{6}$,AC=2,求△ABC的面积.
分析 利用勾股定理得出AB2+BC2=AC2,再根据完全平方公式求出AB•BC=3+2$\sqrt{6}$,那么S△ABC=$\frac{1}{2}$AB•BC,代入计算即可.
解答  解:∵在△ABC中,∠B=90°,
解:∵在△ABC中,∠B=90°,
∴AB2+BC2=AC2,
∴(AB+BC)2-2AB•BC=AC2,
∵AB+BC=2+$\sqrt{6}$,AC=2,
∴(2+$\sqrt{6}$)2-2AB•BC=22,
∴AB•BC=3+2$\sqrt{6}$,
∴S△ABC=$\frac{1}{2}$AB•BC=$\frac{3}{2}$+$\sqrt{6}$.
点评 此题主要考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,也考查了完全平方公式与三角形的面积.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
8.$\sqrt{25}$表示的意义是( )
| A. | 25的立方根 | B. | 25的平方根 | C. | 25的算术平方根 | D. | 5的算术平方根 |
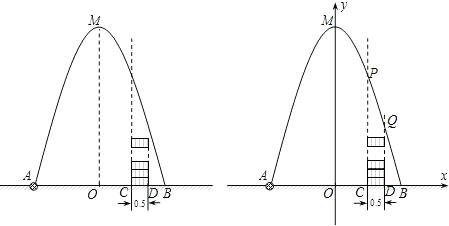
10. 如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )
如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )
 如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )
如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |