��Ŀ����
����Ŀ���侯սʿ��һ����۴�![]() ���������ϣ�ǰ��
���������ϣ�ǰ��![]() ��Ӫ������Ⱥ�ڣ�;��
��Ӫ������Ⱥ�ڣ�;��![]() ��ʱ������Я���ľ���ͧ��
��ʱ������Я���ľ���ͧ��![]() ������Ⱥ���˻�
������Ⱥ���˻�![]() �أ�����ۼ���ǰ������
�أ�����ۼ���ǰ������![]() �ؽӵ�Ⱥ�ں����̷���
�ؽӵ�Ⱥ�ں����̷���![]() �أ�;���������ͧ����������ۺ;���ͧ��
�أ�;���������ͧ����������ۺ;���ͧ��![]() �صľ���
�صľ���![]() ��ǧ�ף��ͳ���۳���������ʱ��
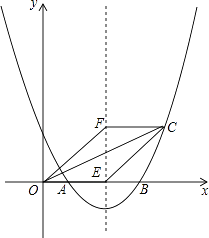
��ǧ�ף��ͳ���۳���������ʱ��![]() ���֣�֮��ĺ���ͼ����ͼ��ʾ������Ӫ��Ⱥ�ڵ�ʱ����Բ��ƣ�ˮ���ٶȺͳ�����ھ�ˮ�е��ٶȲ��䣮
���֣�֮��ĺ���ͼ����ͼ��ʾ������Ӫ��Ⱥ�ڵ�ʱ����Բ��ƣ�ˮ���ٶȺͳ�����ھ�ˮ�е��ٶȲ��䣮

��1����ֱ��д������۴�![]() �ص�
�ص�![]() �����õ�ʱ�䣮
�����õ�ʱ�䣮
��2����ˮ�����ٶȣ�
��3������۽�![]() ��Ⱥ�ڰ�ȫ�͵�
��Ⱥ�ڰ�ȫ�͵�![]() �غ�������ȥ��Ӧ����ͧ����֪����ͧ��
�غ�������ȥ��Ӧ����ͧ����֪����ͧ��![]() �صľ���
�صľ���![]() ��ǧ�ף��ͳ���۳���������ʱ��
��ǧ�ף��ͳ���۳���������ʱ��![]() ���֣�֮��ĺ�����ϵʽΪ
���֣�֮��ĺ�����ϵʽΪ![]() ������Ⱥ�����´���ʱ�䲻�ƣ��������ھ���
������Ⱥ�����´���ʱ�䲻�ƣ��������ھ���![]() �ض�Զ�������ͧ�ڶ���������
�ض�Զ�������ͧ�ڶ���������
���𰸡���1��24���ӣ�2��![]() ǧ��/�֣�3��
ǧ��/�֣�3��![]() ǧ��
ǧ��
��������
��1������λ�Ƴ��Ե��ٶȿ�֪����۴�A�ص�C�����õ�ʱ�䡣
��2����ˮ���ٶ�Ϊaǧ��/�֣�������ٶ�Ϊbǧ��/�֣���������ù���a,b�Ĺ�ϵʽ���ⷽ����õ���
��3����Ϊ����ۺ�ˮ�����ٶȲ��䣬�������߶�a����ֱ�ߵĺ�������ʽΪ
![]() Ȼ�����㣨44,0���Ϳ��Եõ����ۡ�
Ȼ�����㣨44,0���Ϳ��Եõ����ۡ�
�⣺��1��24����
��2����ˮ���ٶ�Ϊ![]() ǧ��/�֣�������ٶ�Ϊ
ǧ��/�֣�������ٶ�Ϊ![]() ǧ��/�֣����������
ǧ��/�֣����������
![]()
���
��ˮ���ٶ���![]() ǧ��/�֣�
ǧ��/�֣�
��3����ͼ����Ϊ����ۺ�ˮ�����ٶȲ��䣬�������߶�![]() ����ֱ�ߵĺ�������ʽΪ
����ֱ�ߵĺ�������ʽΪ

![]()
��![]() ���룬��
���룬��![]()
![]() �߶�
�߶�![]() ����ֱ�ߵĺ�������ʽΪ
����ֱ�ߵĺ�������ʽΪ![]() ��
��
�� ���
���![]() ��һ���������
��һ���������
![]() ������ھ���
������ھ���![]() ��
��![]() ǧ�״������ͧ�ڶ���������
ǧ�״������ͧ�ڶ���������
��������Ҫ�ǿ�����λ�����ٶȵĹ�ϵʽ������Լ���������ʽ�������ۺ����á�

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�����Ŀ��ijУΪ���˽�ѧ����μ�����������������ȡ��50��ѧ��ÿ���������Ĵ�������ͳ�ƣ���ͳ�ƽ�����Ƴ������ֱ��ͼ��
���� | 70��x��90 | 90��x��110 | 110��x��130 | 130��x��150 | 150��x��170 |
���� | 8 | 23 | 16 | 2 | 1 |
����������Ϣ���ش��������⣺
��1��������������������
��2�����ε�����ÿ�������������ﵽ110�����ϣ���110�Σ��Ĺ��еĹ����ˣ�
��3�������ϱ������ݲ�ȫֱ��ͼ��
��4��������������ﵽ130�����ϵ�3������2��Ů����һ��������ѧУ����3���г�ȡ2��ѧ�����о��齻������ǡ�ó���һ��һŮ�ĸ��ʣ�Ҫ�����б�������״ͼд���������̣���