Question

抛物线的顶点坐标为（-2，3），且与x轴交于（x₁，0），（x₂，0），且|x₁-x₂|=6，则此二次函数的解析式为________．

Answer 1

分析：根据抛物线的顶点坐标公式，知=3，则b²-4ac=-12a；根据坐标轴上两点间的距离和一元二次方程的两根，可知|x₁-x₂|=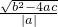=6，从而得36a²=-12a，求得a的值后，即可代入顶点式．
解答：设抛物线的解析式是y=a（x+2）²+3．
根据抛物线的顶点坐标公式，知=3，则b²-4ac=-12a；
根据坐标轴上两点间的距离和一元二次方程的两根，可知|x₁-x₂|=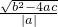=6，
从而得36a²=-12a，
a=0（舍去），a=-．
故答案为y=-（x+2）²+3．
点评：此题综合运用了抛物线的顶点坐标公式和抛物线与x轴的两交点的距离公式．