题目内容
 如图,已知菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D 重合)分别向直线AB、AD作垂线,垂足分别为E、F.
如图,已知菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D 重合)分别向直线AB、AD作垂线,垂足分别为E、F.
(1)BD的长是______;
(2)连接PC,当PE+PF+PC取得最小值时,此时PB的长是______.
解:(1)连接AC,交BD与点O,

∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形,AC=AB=8,
根据菱形性质得:AO=CO= AC=4,OB=OD,AC⊥BD,
AC=4,OB=OD,AC⊥BD,
根据勾股定理得:BD=2OB=2× =8
=8 ;
;
(2)延长FP交BC于点M,则FM⊥BC.

∵PM=PE,
∴PE+PF=PF+PM=FM,
又∵S菱形ABCD=AC•BD=BC•FM,
∴ ×8×8
×8×8 =8•FM,即FM=4
=8•FM,即FM=4 ,
,
∴要使PE+PF+PC取最小值,只要PC取最小值.
当CP⊥BD,即点P与点O重合时,PE+PF+PC的值最小.
此时PB=BO=DO= BD=4
BD=4 .
.
故答案为:8 ;4
;4 .
.
分析:(1)连接AC,交BD与点O,因为菱形ABCD中,∠ABC=60°,可知△ABC为等边三角形,AC=AB=8,根据菱形性质求出AO长,OB=OD,AC⊥BD,根据勾股定理求出BO,即可求出BD;
(2)延长FP交BC于点M,FM⊥BC.根据角平分线的性质求得PM=PE,由菱形的面积求得FM的长度,所以要使PE+PF+PC取最小值,只要PC取最小值.当CP⊥BD,即点P与点O重合时,PE+PF+PC的值最小,求出此时PB的长即可.
点评:本题考查菱形的性质,第一问的解题关键是利用菱形的性质得出△ABC为等边三角形;第二问的解题关键是利用轴对称的性质得出PE+PF=PF+PM=FM,此题有一定的难度.

∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形,AC=AB=8,
根据菱形性质得:AO=CO=
 AC=4,OB=OD,AC⊥BD,
AC=4,OB=OD,AC⊥BD,根据勾股定理得:BD=2OB=2×
 =8
=8 ;
;(2)延长FP交BC于点M,则FM⊥BC.

∵PM=PE,
∴PE+PF=PF+PM=FM,
又∵S菱形ABCD=AC•BD=BC•FM,
∴
 ×8×8
×8×8 =8•FM,即FM=4
=8•FM,即FM=4 ,
,∴要使PE+PF+PC取最小值,只要PC取最小值.
当CP⊥BD,即点P与点O重合时,PE+PF+PC的值最小.
此时PB=BO=DO=
 BD=4
BD=4 .
.故答案为:8
 ;4
;4 .
.分析:(1)连接AC,交BD与点O,因为菱形ABCD中,∠ABC=60°,可知△ABC为等边三角形,AC=AB=8,根据菱形性质求出AO长,OB=OD,AC⊥BD,根据勾股定理求出BO,即可求出BD;
(2)延长FP交BC于点M,FM⊥BC.根据角平分线的性质求得PM=PE,由菱形的面积求得FM的长度,所以要使PE+PF+PC取最小值,只要PC取最小值.当CP⊥BD,即点P与点O重合时,PE+PF+PC的值最小,求出此时PB的长即可.
点评:本题考查菱形的性质,第一问的解题关键是利用菱形的性质得出△ABC为等边三角形;第二问的解题关键是利用轴对称的性质得出PE+PF=PF+PM=FM,此题有一定的难度.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
如图,已知菱形ABCD的边长为1.5cm,B,C两点在扇形AEF的
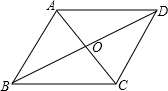 如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
如图,已知菱形ABCD的周长为16cm,∠ABC=60°,对角线AC和BD相交于点O,求AC和BD的长.
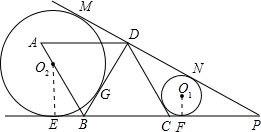 上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.
上,半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N,半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G.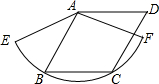 如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的
如图,已知菱形ABCD为2cm.B、C两点在以点A为圆心的