题目内容
 如图,直线y=kx-2(k>2)与双曲线y=
如图,直线y=kx-2(k>2)与双曲线y=| k |
| x |
A、
| ||
| B、2 | ||
| C、8 | ||
D、2
|
分析:根据y=kx-2(k>2)表示出直线与坐标轴的交点,即可得出△OPQ∽△MRP,进而得出△OPQ与△PRM的面积相等,得出△OPQ≌△MRP,从而可以表示出R点的坐标,进而求出答案.
解答:解:直线y=kx-2(k>2)与双曲线y=
在第一象限内的交点R,
与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,且△OPQ与△PRM的面积相等,
∴Q点的坐标为:(0,-2),
0=kx-2,
x=
,
P点的坐标为:(
,0),
∴OQ=2,OP=
,
∵∠RPM=∠OPQ,∠RMP=∠QOP,
∴△OPQ∽△MRP,
∵△OPQ与△PRM的面积相等,
∴△OPQ≌△MRP,
∴PM=OP,RM=OQ,
∴R点的坐标为:(
,2),
∴
×2=k,
解得:k=±2
.
∵k>2,
∴k=2
.
故选D.
| k |
| x |
与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,且△OPQ与△PRM的面积相等,
∴Q点的坐标为:(0,-2),
0=kx-2,
x=
| 2 |
| k |
P点的坐标为:(
| 2 |
| k |
∴OQ=2,OP=
| 2 |
| k |
∵∠RPM=∠OPQ,∠RMP=∠QOP,
∴△OPQ∽△MRP,
∵△OPQ与△PRM的面积相等,
∴△OPQ≌△MRP,
∴PM=OP,RM=OQ,
∴R点的坐标为:(
| 4 |
| k |
∴
| 4 |
| k |
解得:k=±2
| 2 |
∵k>2,
∴k=2
| 2 |
故选D.
点评:此题主要考查了反比例函数的性质,得出△OPQ≌△MRP,PM=OP,RM=OQ,是解决问题的关键.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
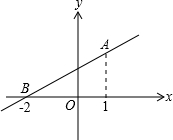 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为