��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A����Ϊ����2![]() ��0������OAB=90������AOB=30��������OAB�Ƶ�O��˳ʱ�뷽����ת����ת��Ϊ����0��������150����������ת�����У���A��B�Ķ�Ӧ��ֱ�Ϊ��A����B����
��0������OAB=90������AOB=30��������OAB�Ƶ�O��˳ʱ�뷽����ת����ת��Ϊ����0��������150����������ת�����У���A��B�Ķ�Ӧ��ֱ�Ϊ��A����B����
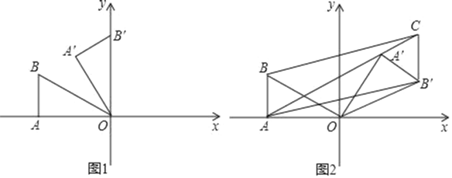
��1����ͼ1������=60��ʱ��ֱ��д����A���� ����B���� �������ꣻ
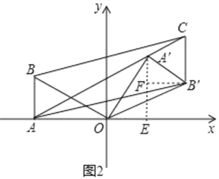
��2����ͼ2������=135��ʱ������B����AB��ƽ���߽�AA���ӳ����ڵ�C������BC��AB����
���ж��ı���AB��CB����״����˵�����ɣ�
�����ʱ��A���͵�B�������ꣻ
��3��������30����ת��150��ʱ����2���е��߶�B��CҲ��֮�ƶ��������B��C��ɨ����������������ֱ��д��������ɣ���
���𰸡���1������![]() ��3������0��4������2�����ı���AB��CB��ƽ���ı��Σ������������A����
��3������0��4������2�����ı���AB��CB��ƽ���ı��Σ������������A����![]() ��
��![]() ������B����
������B����![]() +
+![]() ��
��![]() ��
��![]() ������3��12
������3��12
��������
��1����ͼ1�У���A��E��OB����E����ֱ�����������EO��A��E���ɽ�����⣻
��2������ͼ2�У����ۣ��ı���AB��CB��ƽ���ı��Σ�ֻҪ֤��B��C��AB��B��C=AB��
�ڹ���A����A��E��x����E������B����B��F��A��E��F����ֱ�����������OE��EF��B��F���ɣ�
��3��B��Cɨ�������=Sƽ���ı���B��B��C��C�����ɴ˼��㼴�ɣ�
�⣺��1����ͼ1�У���A��E��OB����E��
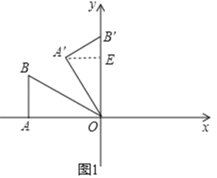
��Rt����OA��B���У��ߡ�A��OB��=30����OA��=2![]() ��
��
��cos30��=![]() ��
��
��OB��=4��
��B����0��4����
��Rt��OA��E����OA��=2![]() ��
��
��A��E=![]() ��OE=
��OE=![]() A��E=3��
A��E=3��
��A������![]() ��3����
��3����
�ʴ�Ϊ����![]() ��3������0��4����
��3������0��4����
��2������ͼ2�У����ۣ��ı���AB��CB��ƽ���ı��Σ�
���ɣ���B��C��AB��
���B��CA=��BAC��
�ߡ�BAC+��CAO=90����
���B��CA��+��CAO=90����
�֡ߡ�B��A��C+��OA��A=90��������ת�õ�OA=OA�������CAO=��OA��A��
���B��CA��=��B��A��C��
��B��C=B��A����
�֡�A��B��=AB��
��B��C=AB��
���ı���AB��CB��ƽ���ı��Σ�
�ڹ���A����A��E��x����E��
��A����2![]() ��0�����ɵ�OA=2
��0�����ɵ�OA=2![]() ��
��
�֡ߡ�OAB=90������AOB=30����
��AB=2��OB=4����OA��=2![]() ��A��B��=2��
��A��B��=2��
�ɡ�AOA��=135�����õ���A��OE=45����
��OE=A��E=![]() OA��=
OA��=![]() ��
��
���A����![]() ��
��![]() ����
����
����B����B��F��A��E��F��
�ɡ�EA��O=45�����á�EA��B��=45����
��B��F=A��F=![]() ��2=
��2=![]() ��
��
��EF=![]() ��
��![]() ��OE+B��F=
��OE+B��F=![]() +
+![]() ��
��
���B����![]() +
+![]() ��
��![]() ��
��![]() ����
����
��3����ͼ3�У���ϣ�2��֪��
��![]() ʱ��
ʱ��![]() ��
��
![]() �ϵĸ�Ϊ
�ϵĸ�Ϊ![]()
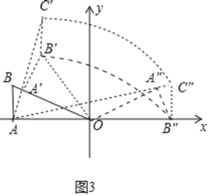
B��Cɨ�������=Sƽ���ı���B��B��C��C��=6��2=12��