题目内容
 如图,△ABC中,分别在AB、AC上取点D、E,使得BD=CE,连结BE、CD相交于点P,点M是BC的中点,∠BAC的平分线AQ与PM相交于点Q.求证:四边形BPCQ是平行四边形.
如图,△ABC中,分别在AB、AC上取点D、E,使得BD=CE,连结BE、CD相交于点P,点M是BC的中点,∠BAC的平分线AQ与PM相交于点Q.求证:四边形BPCQ是平行四边形.考点:平行四边形的判定
专题:证明题
分析:在射线PM上取Q',使PM=MQ',连AQ',BQ',CQ',DQ',EQ'.易证BPCQ'是平行四边形,利用平行四边形的性质和三角形面积间的数量关系推知Q'到AB的距离=Q'到AC的距离,则Q'在∠BAC的平分线AQ上,所以Q'与Q重合.故四边形BPCQ即四边形BPCQ'为平行四边形.
解答: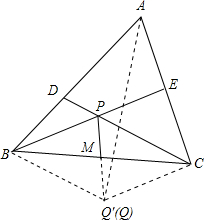 解:在射线PM上取Q',使PM=MQ',连AQ',BQ',CQ',DQ',EQ'.
解:在射线PM上取Q',使PM=MQ',连AQ',BQ',CQ',DQ',EQ'.
∵BM=MC,PM=MQ',
∴BPCQ'是平行四边形,即有CP∥BQ',BP∥CQ',
∴S△DBQ'=S△CBQ'=S△CEQ'.
又∵BD=CE,
∴Q'到AB的距离=2•
=2•
=Q'到AC的距离,
∴Q'在∠BAC的平分线AQ上.
于是Q'为PM与AQ的交点,即Q'与Q重合.
故四边形BPCQ即四边形BPCQ'为平行四边形.
 解:在射线PM上取Q',使PM=MQ',连AQ',BQ',CQ',DQ',EQ'.
解:在射线PM上取Q',使PM=MQ',连AQ',BQ',CQ',DQ',EQ'.∵BM=MC,PM=MQ',
∴BPCQ'是平行四边形,即有CP∥BQ',BP∥CQ',
∴S△DBQ'=S△CBQ'=S△CEQ'.
又∵BD=CE,
∴Q'到AB的距离=2•
| S△DBQ′ |
| BD |
| S△CEQ′ |
| CE |
∴Q'在∠BAC的平分线AQ上.
于是Q'为PM与AQ的交点,即Q'与Q重合.
故四边形BPCQ即四边形BPCQ'为平行四边形.
点评:本题考查了平行四边形判定.此题实际上是利用了逆证法推知四边形BPCQ为平行四边形的.

练习册系列答案
相关题目
 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠2=20°,则∠1=
如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠2=20°,则∠1= 如图,沿着边长为90cm的正方形,按照A-B-C-D-A…的方向,电子蚂蚁甲从A以65cm/min的速度前进,电子蚂蚁乙同时从A以72cm/min的速度前进.
如图,沿着边长为90cm的正方形,按照A-B-C-D-A…的方向,电子蚂蚁甲从A以65cm/min的速度前进,电子蚂蚁乙同时从A以72cm/min的速度前进.