题目内容
【题目】对于任意一个四位数
．如果把它的前两位数字和后两位数字调换，则称得到的数为的调换数，把与其调换数之差记为
，例如
的调换数为
，
．
（1）求证：对于任意
一个四位数，都能被
整除．
（2）我们把与的商记为，例如
，若有两数
、
，其中
， 
，
，
、
都是正整数)，那么当
时，求
的最大值．
【答案】（1）详见解析；（2）60
【解析】
(1)设任意一个四位数
的千位、百位、十位、个位数字分别为
、
、
、
，分别表示出这个四位数与其调换数，将这两个数作差化简即可得到结论；
(2)根据题目意思分别表示出
和
，将和代入
得出
，再表示出
，结合题目条件即可得出结果．
(1)证明：设任意一个四位数的千位、百位、十位、个位数字分别为、、、，则
、、、为自然数，
为自然数，
能被
整除；
(2)解：由题意可得：
，
，
，开口向下，且对称轴为
又
，且
为正整数，
当
时，取得最大值
．
练习册系列答案
相关题目
【题目】阅读下面内容，并按要求解决问题：
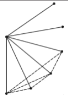
问题：“在平面内，已知分别有2个点，3个点，4个点，5个点，…，
个点，其中任意三个点都不在同一条直线上经过每两点画一条直线，它们可以分别画多少条直线？”
探究：为了解决这个问题，希望小组的同学们，设计了如下表格进行探究：（为了方便研究问题，图中每条线段表示过线段两端点的一条直线）
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题：
（1）请帮助希望小组归纳，并直接写出结论：当平面内有个点时，直线条数为______；
（2）若某同学按照本题中的方法，共画了28条直线，求该平面内有多少个已知点？
