题目内容
已知某商品销售利润y(元)与该商品销售单价x(个)满足y=-20x2+1400x-2000,则该商品获利最多为 元.
考点:二次函数的应用
专题:
分析:由题意知利润y(元)与销售的单价x(元)之间的关系式,化为顶点式求出y的最大值.
解答:解:利润y(元)与销售的单价x(元)之间的关系为
y=-20x2+1400x-2000=-20(x-35)2+22500.
∵-20<0
∴当x=35元时,y最大为22500元.
即该商品获利最多为22500元.
故答案为:22500.
y=-20x2+1400x-2000=-20(x-35)2+22500.
∵-20<0
∴当x=35元时,y最大为22500元.
即该商品获利最多为22500元.
故答案为:22500.
点评:本题考查二次函数的实际应用,借助二次函数的顶点式解决实际问题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知a、b都是有理数,且(a+1)2+|b-2014|=0,则ab等于( )
| A、3 | B、-1 | C、1 | D、5 |
 如图,⊙O是直径BC,弦AB,∠BAC的平分线交⊙O于点D.
如图,⊙O是直径BC,弦AB,∠BAC的平分线交⊙O于点D. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点). 小明站在距离篮筐的水平距离5米的O处进行投篮试验,球的运动路线是抛物线y=-
小明站在距离篮筐的水平距离5米的O处进行投篮试验,球的运动路线是抛物线y=-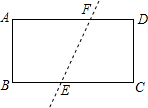 已知,如图,在矩形(两组对边平行且相等,四个内角都为直角)ABCD中,AB=4,BC=8,把它沿直线EF折叠,点C与点A重合,求CE的长.
已知,如图,在矩形(两组对边平行且相等,四个内角都为直角)ABCD中,AB=4,BC=8,把它沿直线EF折叠,点C与点A重合,求CE的长.